CHAPTER 5
Dose-Response, Linear Regression,
Part 1. Radiation-Induced Cancer: The "Build-Up" Phase Part 2. Equilibrium Phase: Flat Rates of Radiation-Induced Cancer Part 3. The "Build-Down" Phase: An Exceedingly Gradual Phenomenon Part 4. Is There Really Any "Minimum Latency Period" ? Part 5. Dose-Response: Linearity and Regression Analysis Part 6. Dose-Response: Perfect Correlation without Perfect Proportionality Part 7. Dose-Response: Effects of Imperfect Matching across Dose-Groups Part 8. Real-World "Entropic Circumstances" Which Reduce Observed Correlations Part 9. Estimating the Impact of Medical Radiation on Cancer MortRates
Figure 5-A. Annual Delivery-Rates of Radiation-Induced Cancer. Figure 5-B. The MX Model of Dose-Response. Figure 5-C. The MX+C Model of Dose-Response. Figure 5-D. Effect of Imperfect Matching of Dose-Groups. Figure 5-E. Effect of an Inverse Relationship between Dose and a Co-Actor.
* Part 1. Radiation-Induced Cancer: The "Build-Up" Years
Because ionizing radiation is a carcinogen (Chapter 2, Part 4), its introduction into medicine, in 1896, had to cause radiation-induced Cancers. The Cancers, caused by medical radiation received during 1896, did not all appear at once. Like products dispensed from an inventory, the Cancers were delivered gradually (Chapter 2, Part 8). And the Cancers caused by medical radiation received during 1897 were also delivered gradually. And the Cancers caused by medical radiation received during 1898 were gradually delivered, too. We need not name every year for a century.
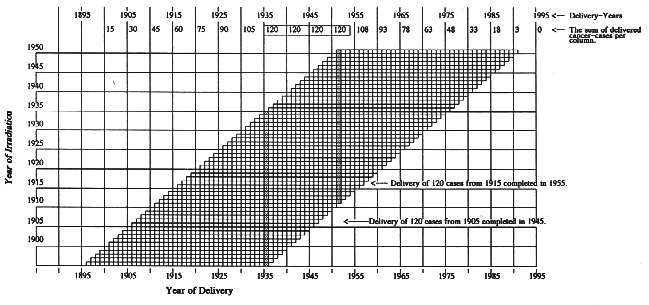
1a. Figure 5-A: The "Build-Up" Years
Figure 5-A depicts the effect of gradual delivery: A period of "build-up" in the annual delivery of radiation-induced Cancer. Figure 5-A refers to cancer incidence, with no arbitrary interval between radiation exposure and diagnosis of radiation-induced cancer (discussion in Part 4, below). We emphasize that Figure 5-A is a diagram in which we arbitrarily:
(a) show years of annual irradiation only through 1951;
(b) make 120 cases (per 100,000 population) the total cancer-consequence from each year's irradiation;
(c) make 40 years the maximum delivery-time for the 120 cases produced by a single year's irradiation;
(d) make delivery of the 120 cases occur at a constant annual rate: 3 cases per 100,000 population, annually, for 40 years. This is equivalent to having 40 different latency periods before diagnosis occurs.As a result of these choices, the annual deliveries of Cancer induced by medical irradiation show a build-up in Figure 5-A as follows:
During 1896: 3 cases delivered per 100,000 population.
During 1897: 6 cases delivered per 100,000 population.
During 1898: 9 cases delivered per 100,000 population.
During 1899: 12 cases delivered per 100,000 population.
During 1900: 15 cases delivered per 100,000 population.
..... The 40th year is 1935.
During 1935: 120 cases delivered per 100,000 population.Although the numbers in Figure 5-A are merely illustrative, they make a key point: The introduction and maintenance of medical radiation necessarily caused a gradual build-up in the number of radiation-induced cases of Cancer per 100,000 population.
1b. Equality of Response: A Simplifying Assumption in Figure 5-A
Figure 5-A depicts an "ideal" situation in which the magnitude of the average radiation dose is the same every year, and the magnitude of the response is the same (120 radiation-induced Cancers per 100,000 population).
Equality of response over decades is a condition invoked for simplification. In reality, several lines of evidence indicate that the magnitude of carcinogenic response, per rad of radiation exposure, can be modulated (altered) by the intensity of exposure to nonradiation co-actors and by the absence of such co-actors. Therefore, the magnitude of cancer-response, per unit of radiation exposure, can vary over time according to the abundance or paucity of co-actors.
The Introduction has already discussed the widely accepted concept that more than one cause is necessary to produce a case of fatal Cancer. Ways in which carcinogenic co-actors can multiply each other's potency is a topic deferred to Chapters 49, 67, and Appendix-M. Here, we simply point out that --- when Figure 5-A depicts a response of constant size to a radiation dose of constant size, decade after decade --- we have invoked the "ideal" assumption that exposure to co-actors is also constant decade after decade.
* Part 2. Equilibrium Years: Flat Rates of Radiation-Induced Cancer
When the production-rate and the delivery-rate of Cancer are equal in the same calendar year --- despite the variable and extended latency periods --- it is because equilibrium has occurred between two opposite drives. During the equilibrium years, successive columns add one box at the top --- and subtract one box at the bottom.
Equilibrium is first reached in Figure 5-A in the year 1935. That is the first year in which 120 new Cancers/100,000 population are produced (for gradual delivery) and also 120 radiation-induced Cancers are delivered (from earlier years of production plus 1935 production).
Since nothing changes in our ideal model, Figure 5-A shows that equilibrium continues through 1951. Equilibrium would continue indefinitely if the average radiation dose were maintained at a constant level "forever" --- but due to the size of our page, Figure 5-A completely terminates medical irradiation after 1951.
Flat Cancer-Rates and the "Law of Equality"
The "Law of Equality" states: If an age-matched population receives the same level of irradiation and same exposure to co-actors year after year, ultimately a state of equilibrium will be reached when the annual delivery-rate of radiation-induced Cancer per 100,000 population is equal to the annual production-rate of radiation-induced Cancer per 100,000 population, and the same annual delivery-rate will endure indefinitely, if the same annual production-rate is maintained.
In other words, the "Law of Equality" leads toward flat rates of radiation-induced Cancer. In Figure 5-A, the rate in every year of equilibrium is 120 cases/100,000 population. The equilibrium years, in Figure 5-A, are limited to 1935 through 1951 --- simply because of the size of the page.
Does the "Law of Equality" depend on assuming that the delivery rate of a single year's production occurs in equal parts --- such as 3 cases each year as shown in Figure 5-A? No. The law is also valid for delivery in unequal parts over the specified timespan. This is demonstrated in Gofman 1995/96, where all of Chapter 4 is devoted to the "Law of Equality."
* Part 3. The "Build-Down" Phase: An Exceedingly Gradual Phenomenon
Due to the size of our page, Figure 5-A completely terminates irradiation of the population after 1951. But deliveries of radiation-induced Cancer continue, because in 1951, deliveries from irradiation received during the 1940s and 1930s and 1920s and even earlier, were not yet complete. The total annual deliveries can decline only gradually, even when there is no additional production.
The build-down of deliveries can be quantified by counting the vertical boxes in the post-1951 columns. Each year, just one box is coming off at the bottom of successive columns. So total delivery declines to 117 cases in 1952, 114 cases in 1953, 111 cases in 1952, and so forth.
3a. How Does the "Termination" Model Relate to Reality?
Depiction of this build-down phase should drive home an important point. If all medical radiation were abruptly and permanently terminated (which we certainly do not advocate), and if exposure to co-carcinogens were held constant, the resulting reduction in cancer mortality rates would happen gradually over about 50 years --- due to delivery of radiation-induced cases already "in the pipeline." The gradual build-down depicted in Figure 5-A is an important reminder, that uselessly high doses of xrays administered today will still be causing Cancers 10, 20, 30, 40 (and more) years from now.
3b. Real-World Status of Delivery-Schedules
For radiation-induced cancer cases, delivery-intervals after irradiation are necessarily much clearer in studies of excess cases due to exposure at a single time (such as radio-iodine exposure from the Chernobyl accident, or gamma-ray exposure from the Hiroshima-Nagasaki bombs), than in studies of excess Cancer due to chronic exposure (such as occupational exposures spread over years or decades). In the latter, it is impossible to know in which years the radiation produced the carcinogenic lesions. Thus, analysts rely heavily on the Atomic-Bomb Study for our knowledge of delivery-intervals and duration (Chapter 2, Part 8).
The observation, of excess Cancers (meaning radiation-induced cases) from a particular radiation event, refers to the excess number compared with the number occurring in comparable "control" groups not exposed to extra radiation from the particular radiation event. Of course, part of the "background" cancer-rate in the control groups is radiation-induced too --- by other sources of radiation exposure.
The total cancer-rate (radiation-induced cases plus cases which would occur anyway) climbs with advancing age --- as illustrated for 1940 in Chapter 4 (Box 2), and for 1990 in Chapter 4 (Box 4). To the extent that radiation-induced cases occur at approximately the same ages as radiation-unaided cases (Gofman 1971, p.244; BEIR 1990, p.5), then the average interval between irradiation and delivery of radiation-induced cases will be longer for cases induced during childhood than for cases induced at ages near or beyond age 55.
Even though delivery-schedules vary by age at irradiation, delivery-schedules for radiation-induced Cancers will be the same, per 100,000 population, in all Nine Census Divisions --- because the Divisions have been "matched" for age by use of age-adjusted cancer MortRates.
* Part 4. Is There Really Any "Minimum Latency Period" ?
The notion that there exists a "minimum latency period" of 5 to 20 years after radiation exposure, before any radiation-induced Cancer is manifest, is almost certainly mistaken (Gofman 1981, Gofman 1994, Gofman 1995/96). The limited evidence at hand shows that atomic-bomb-induced Leukemia showed up before five years (BEIR 1972, p.101; and UNSCEAR 1986, p.222, Fig. 24), and that Chernobyl-induced Thyroid Cancer also showed up within five years (Kazakov 1992; Baverstock 1992; WHO 1995).
Indeed, in a non-Chernobyl radio-iodine study (of 38,000 medical patients who received diagnostic doses of iodine-131), Holm et al mention a large excess of Thyroid Cancer observed during the first five years after administration of the iodine-131 (Holm 1988). However, Holm et al count none of these Cancers as caused by the radio-iodine. With a single sentence, the cases are simply discarded from the study --- a decision which appears to be a highly questionable prejudgment (full analysis in Gofman 1990, Chapter 22, Part 5).
After the atomic bombings in August 1945, the A-Bomb Survivors Study is silent about solid Cancers until 1950. The study's first report on solid Cancers covers the period 1950 through 1954. It shows that, by then, the 25,203 exposed survivors (all ages and all doses, combined) had a solid cancer MortRate which was already 11% higher than the rate among the 66,028 participants in the reference-group (details in Gofman 1990, Table 17-A). If the study had involved 130,000,000 to 250,000,000 participants --- as our study of the entire U.S. population does --- then a radiation-induced excess MortRate of fatal solid Cancers might have been detectable within 1 to 2 years after the bombings.
We know of no studies which are capable of establishing that a five-year "minimum latency period" truly occurs, between exposure of a mixed-age population to extra ionizing radiation and delivery of fatal cases of radiation-induced solid Cancers.
Some Biology-Based Logic for Expecting No Minimum
We know of no biological basis for expecting any minimum latency period for Cancer in a large mixed-age population. By contrast, we know of some reasons for expecting no such minimum.
In molecular biology, evidence is accumulating that a cell becomes malignant only after its chromosomes have accumulated several carcinogenic abnormalities (see Appendix D, for instance). Some of these genetic abnormalities may be inherited, and others may be acquired at any age after conception. If a cell, which has already accumulated a full set of carcinogenic lesions except for one, receives the final necessary lesion from a radiation-exposure, the delivery-time for that particular case of radiation-induced Cancer could be extremely short.
Almost certainly, carcinogenic genetic lesions have a range of effects, from a mild predisposition to Cancer, to a virtual guarantee of a rapidly lethal malignancy. It is very reasonable to expect that the speed of cancer development varies with the particular areas of chromosomal damage or chromosomal deletion which are present in a cell. For this reason, too, it is very reasonable to expect that some radiation-induced Cancers will be delivered almost immediately as overt, clinical cases.
Unless strong epidemiologic evidence develops someday in favor of a minimum latency period for radiation-induced Cancers, we think the most reasonable assumption is no minimum latency period in populations of mixed ages.
* Part 5. Dose-Response: Linearity and Regression Analysis
In Figures 1-A and 1-B of Chapter 1, the boxy symbols show the nine pairs of PhysPop values and MortRates (one pair for each of the Nine Census Divisions). Those PhysPop values and MortRates have a strong linear relationship with each other --- which is clear because the boxy symbols cluster so closely around a straight line. If this were a perfect linear correlation, the boxy symbols would fall directly upon a single straight line, with no scatter at all.
5a. The Linear Dose-Response: Meaning and Expression
In a perfect linear relationship, one additional unit of dose adds exactly the same number of fatal cases to the MortRate, no matter whether the total dose is low or high. Suppose that each dose-unit adds 6 fatal cancers to the cancer MortRate. Then 3 additional units of dose will add 18 fatal Cancers to the MortRate. Thus, increment in MortRate (18 cases) is proportional to the increment in dose (3 units), and the constant of proportionality (which relates dose to MortRate) is 6 cases per unit of dose. 18 additional fatal cases = (6 additional cases / dose-unit) times (3 additional dose-units). The dose-units cancel out in this equation, so that additional cases = additional cases.
When dose-response is linear, each MortRate is related to its corresponding dose by the equation for a straight line: y = mx + c.
o The y-variable is the MortRate, expressed in "cases per 100,000 population," for example.
o The x-variable is the corresponding dose, expressed in dose-units (for example, in PhysPop values in this book).
o "m" is the coefficient of proportionality (also called the X-Coefficient), expressed as "fatal cases per dose-unit." Thus, potency per dose-unit is the same at all dose-levels.
o "c" is a Constant, expressed in the same MortRate units as "y." The Constant quantifies the number of cases in the total MortRate which are not related to dose.When the value of the Constant is greater than zero, then each MortRate is proportional to dose only after the Constant is subtracted from the total MortRate: (y - c) = mx. If the value of the constant is zero, there is nothing to subtract, and the entire MortRate is proportional to dose. In that case, y = mx.
5b. Figure 5-B: Perfect Proportionality (MX Model)
Figure 5-B, which is located at the end of this chapter, illustrates what we call the MX model of dose-response --- an abbreviation of the equation y = mx. This is the model in which the entire MortRate (y) is directly proportional to PhysPop (x). In other words, the MX model reflects the concept that medical radiation became a contributing cause to nearly all cases of fatal Cancer, with nearly no cases unaided by medical radiation.
5c. The X-Values and Y-Values for Figure 5-B (MX Model)
In Figure 5-B, the x-values are the nine real PhysPops of 1940 (from the Universal PhysPop Table 3-A). The y-values are an unreal set of MortRates. We have arbitrarily made the highest MortRate equal to 120 radiation-induced cancers per 100,000 population. Readers have seen that rate before. It is the annual delivery-rate of cancer depicted in Figure 5-A during the equilibrium years. In Figure 5-B, we pair it with the highest 1940 PhysPop value, which is 169.76 in the Mid-Atlantic Division.
To obtain eight other illustrative MortRate values, which must be perfectly proportional in the MX model to the eight other PhysPops of 1940, we do exactly what we did in Chapter 3, Part 6b. We take the ratio of the y-variable over the corresponding x-variable: (120 / 169.76) = 0.7068803. Then we multiply each of the eight PhysPops by 0.7068803 to obtain their matching MortRates --- thus making the pairs of x,y values perfectly proportional to each other (y = mx). The value of m (the X-Coefficient) is 0.7068803.
Some Ratios Resulting from Perfect Proportionality
As a result, the proportionalities demonstrated in Chapter 3, Part 6b, apply here too. We already know that the ratios of the MortRates over the PhysPops are 0.7068803 in every Census Division, because we just made them so. In addition, any two MortRates will have the same ratio as their corresponding PhysPops. For example, we can compare the New England Division with the Mountain Division (data in Figure 5-B). The MortRate ratio is (114.1969 / 84.74820), or 1.347. The corresponding PhysPop ratio is (161.55 / 119.89), or 1.347. The same.
It follows, in the MX model, that the ratio of PhysPop Hi5/Lo4, and the ratio of MortRate Hi5/Lo4, must be the same. (The Hi5/Lo4 ratio was introduced in Chapter 3, Part 4.) From the Universal PhysPop Table 3-A, we find that the Hi5/Lo4 PhysPop ratio for 1940 is 1.46. When we calculate the Hi5 average and the Lo4 average for the synthetic MortRates in Figure 5-B, we obtain 105.68 and 72.53, respectively. Their ratio is also 1.46.
5d. Linearity: Interpreting the Absence of Curvature
Before proceeding to linear regression analysis, we want to comment on the strong linear relationships between MortRates and PhysPop values, already depicted in Figures 1-A and 1-B of Chapter 1. In view of the data discussed in Chapter 2, Part 5b, how do we interpret the observation that these correlations are linear rather than curved?
We refer to the nature of PhysPop itself:
PhysPop is proportional to average accumulated per capita population dose from medical radiation because the more physicians there are per 100,000 population, the more radiation procedures are done per 100,000 persons. The increase in procedures occurs chiefly because more persons per 100,000 receive such attention --- not because the same persons get irradiated more often. In other words, the average per-patient dose is about the same in the Census Divisions with low PhysPop values as in Divisions with high PhysPop values, but the average per-capita dose is higher in high-PhysPop Census Divisions than in low PhysPop Divisions because there are more patients per 100,000 population in high-PhysPop Divisions.
At the cellular level where xray-induced mutations occur, the average per-patient dose-level is likely to be very similar in all Nine Census Divisions. Therefore, the observed absence of curvature (e.g., the absence of supra-linearity) matches expectation, in dose-responses between PhysPop and MortRates.
5e. Linear Regression Analysis: Best-Fit Equation, Best-Fit Line (MX Model)
Regression analysis is a branch of mathematics which can evaluate the correlation between sets of x,y pairs. Part 5a has already emphasized that, in a linear dose-response, each MortRate (y) is related to its corresponding PhysPop (x) by the equation for a straight line: y = mx + b.
In earlier decades, we had to do the calculations for regression analysis by hand. Now, we can just enter the two columns of data (the x-values and the corresponding y-values) into the proper location of a computer spreadsheet, and use a regression-analysis program to do the calculations for us. The program which we use, in the Lotus 123 spreadsheet, produces standard output from the method of least squares. The program is described in the Lotus Journal by Chuck Sullivan, a systems engineer for the Lotus Development Corporation (Sullivan 1986). Every regression analysis has input and output.
Obtaining the Equation of Best Fit, from Figure 5-B
The input-data for the regression analysis of Figure 5-B: The x-values are the nine real 1940 PhysPops, and the y-values are nine corresponding MortRates, calculated in Part 5c in order to illustrate a perfect linear correlation. The additional x-entries and "Best-Fit Calculated MortRates" in Figure 5-B are needed for graphing, as explained below.
The regression output: The output is located at the top-right of Figure 5-B. From it, we obtain the values of the X-Coefficient and the Constant (discussed in Part 5a) which are required in order to write the best-fit equation for this set of data. Patterned on the straight-line equation, y = mx + c, the equation of best fit for Figure 5-B is:
MortRate = (0.7068803 * PhysPop) + Zero. [ * denotes multiplication.]
Generating the line of Best-Fit from the Best-Fit Equation
Using this best-fit equation, we can "plug in" any value for PhysPop, and calculate a corresponding MortRate. Each MortRate requires a separate calculation. To distinguish such MortRates from real-world observations ("observed MortRates"), it is customary to call them "calculated" or "estimated" or "best-fit" MortRates.
By using such calculations, we obtained the column of best-fit MortRates in Figure 5-B --- including MortRates when PhysPop = 90, when PhysPop = 80, when PhysPop = 70 ... right down to PhysPop = 0. The line of best fit, which is graphed in Figure 5-B, connects these pairs of x,y values (various PhysPops, best-fit MortRates).
5f. The X-Coefficient and the Constant (MX Model)
X-Coefficient: Because in Part 5c, we made the pairs of x,y values perfectly proportional to each other (Mort Rate = 0.7068803 times PhysPop, where PhysPop is the x-variable), the regression output had to produce 0.7068803 as the "X-Coefficient." The X-Coefficient is simply "m" in the equation, y = mx. Re-arranged: m = y/x. So "m" evaluates how many units of y (the MortRate) occur per unit of x (dose). In short, the X-Coefficient describes how steep the slope is, of the best-fit line.
Constant: The Constant is "c" in the straight-line equation, y = mx + c. The Constant is the value of y, when x = zero. The value of the Constant (the c-value) never changes --- which gives it the name "Constant." When the x-value changes to a new value, the X-Coefficient ("m") determines the new value of the product, "mx", which gets added to the c-value to produce the new and corresponding best-fit y-value.
In Part 5c, we made every MortRate = (0.7068803 times PhysPop), a procedure for which the equation is y = mx. So, when the resulting pairs of x,y values were fed into the linear regression analysis, there was no "room" for any c-value other than zero in the regression's straight-line equation (y = mx + c). Quite predictably, the regression output in Figure 5-B shows the value of the Constant to be zero.
In the MX model, the Constant has a value of zero, and so the entire value of the MortRate is directly proportional to every corresponding value of PhysPop (Part 5b).
The Y-Axis Intercept and the "Origin"
Because the Constant is the value of y, when x = zero, the Constant is the value of y wherever the best-fit line intercepts the vertical y-axis. Thus, in our graphs, the Constant (also called "the y-intercept") is the value of the mortrate, when the value of physpop is zero. The spot where both y = 0 and x = 0 is called the "origin" in such graphs.
5g. The R-Squared Value and the "Std Err of Coef" (MX Model)
The regression output at top-right of Figure 5-B provides some measures of how good (how strong) the x,y correlation is.
R-Squared Value: The R-squared value measures the "goodness of fit" between the line of best fit and the pairs of input-data. The input-pairs are depicted by the boxy symbols in our graphs. Only a perfect correlation produces an R-squared value of 1.00 from regression analysis, as we emphasized in Chapter 3, Parts 6 and 7. Imperfect correlations generate R-squared values less than 1.00. A rule of thumb is that R-squared values below 0.3 are not considered to be statistically significant (at about the 90% confidence level). As readers study the chapters on non-malignancies in this book, they will see some R-squared values quite a bit lower than 0.3 --- meaning no detectable correlation whatsoever between the x,y pairs.
Standard Error of the X-Coefficient: The Standard Error (SE) of the X-Coefficient is an indicator of how reliable is the slope of the best-fit line. The certainty of a slope and the strength of a correlation diminish as the distance grows between the best-fit line and some of the boxy symbols, of course.
"The smaller, the better," is the rule for the size of the Standard Error (SE) of the X-Coefficient, relative to the size of the X-Coefficient itself. In Figure 5-B, the MX model produces "zero" as the SE of the X-Coefficient, because the slope of the best-fit line is not in any doubt when there is a perfect correlation (R-squared = 1.00).
90% Confidence Limits on the X-Coefficient
The 90% confidence-limits (CLs) on the X-Coefficient are calculated from the SE. The upper limit is (X-Coef) + (1.645 times SE) and the lower limit is (X-Coef) - (1.645 times SE).
For example, if the X-Coefficient from regression output is (0.203) and its Standard Error is (0.045), then (at the 90% CL) the upper limit on the X-Coefficient is (0.203) + (1.645 times 0.045) = (0.203 + 0.074) = (0.277). The lower CL is (0.203) - (1.645 times 0.045) = (0.203 - 0.074) = (0.129). In other words, if a great number of samples were measured and regressed, 90% of the X-Coefficients would fall in the range of 0.129 through 0.277. However, the central value (provided by the regression output) is the most likely value --- and therefore, the central value is often called "the best value."
Ratio of the X-Coefficient over Its Standard Error (SE)
In the example above, the ratio of the X-Coefficient over its SE is (0.203 / 0.045), or 4.51. A rule of thumb is that the value of the X-Coefficient over its SE needs to be at least 2.0 before the X-Coefficient is regarded as reasonably reliable. In our dose-response studies, we will calculate the ratio for each regression. Readers will see see some ratios as high as 5 and higher --- which means that those slopes are highly reliable.
5h. Effect of a Single Deviant Datapoint upon the Constant
Whenever real-world data fit the MX model of dose-response rather closely, but not perfectly, the effect of a single deviant datapoint (boxy symbol) upon the Constant deserves appreciation.
For example, if we move only a high datapoint in Figure 5-B far above the best-fit line, we would need a new regression analysis using the altered input-data. The new regression analysis would produce a steeper slope and a negative Constant, instead of a Constant of zero. The new best-fit line would intersect the vertical y-axis below the origin. We would see a similar result if we had moved a low datapoint to a new location far below the best-fit line. In similar fashion, different "moves" of a single datapoint could tip the slope to be less steep, in which case the Constant of zero (which characterizes perfect proportionality) would rise to a positive value. In real-world data, single "out-lying" datapoints can have such effects.
5i. What Results Would We Expect from Ideal Research Circumstances?
To obtain an overview of the architecture of our dose-response studies, between PhysPop and cancer MortRates, it is useful to imagine that real-world conditions will be "ideal" for such studies.
"Ideal" conditions would resemble the conditions described for Figure 5-A. However, Figure 5-A refers only to one population. Our studies compare the nine different populations in the Nine Census Divisions. "Ideally," there would be no migration among the Census Divisions, and each separate population would receive exposure to a constant annual average per capita dose of medical radiation, decade after decade, with constant levels of co-actors decade after decade.
Under such conditions, what should we expect to observe with respect to the dose-response relationship between PhysPop and cancer MortRates, after the introduction of radiation into medicine in 1896?
We would expect to observe a positive and linear dose-response, by Census Divisions, between the nine MortRates and the nine corresponding PhysPops, decade after decade. If regression analysis produced a Constant greater than zero, we would subtract the Constant from each of the nine Observed MortRates, and we would expect the nine remaining MortRate values to stay always in the same proportions with each other as the fixed proportions among the nine PhysPop values. In other words, we would expect the variation in cause to control the variation in effect.
The same expectation can be expressed somewhat differently. Under ideal research conditions, we would have nine separate populations which never mix from one Census Division to another, and each population would constantly receive its own, fixed, per capita average dose of medical radiation, decade after decade. Each of the nine, different, average per capita doses would produce its own separate stream of radiation-induced Cancers in the population of its own Census Division. Under such conditions, of course we would expect that these nine separate streams of radiation-induced Cancer (expressed as excess age-adjusted cancer MortRates per 100,000 population) would have proportions with each other which mirror the proportions that the nine causal doses of medical radiation have with each other.
It remained for us to learn, just how severely real-world research conditions might depart from the ideal, as we undertook to examine much of a century.
* Part 6. Dose-Response: Perfect Correlation without Perfect Proportionality
In contrast to the MX model of dose-response, the MX+C model reflects the concept that medical radiation does not contribute to every case of fatal Cancer. The Constant quantifies the number of cases which occur without help from medical radiation.
6a. Figure 5-C: One Alteration in the Input Data of Figure 5-B
Figure 5-C, located at the end of this chapter, depicts the MX+C model of dose-response. It is designed to be exactly like Figure 5-B except for one type of alteration. Every MortRate in Figure 5-B has had 20 Cancers (per 100,000 population) added, for Figure 5-C. In other words, we have given the Constant a value of 20. When PhysPop = zero, the cancer MortRate is 20 cases (per 100,000 population). In Figure 5-C, the input-data for the x-variable (the nine PhysPops) are the same as in Figure 5-B.
How does the regression output differ in Figure 5-Cfrom the output in Figure 5-B?
Only the Constant has changed, from zero to 20. But the slope of the best-fit line is still the same, with the X-Coefficient at 0.7068803, and with the standard error still at zero. And the correlation between the pairs of x,y variables is still perfect, with an R-squared value of 1.00.
The equation of best fit is now: MortRate = (0.7068803 times PhysPop) + 20. And with that equation, we calculated MortRates in order to graph the line of best fit. The graph shows the y-intercept at 20, of course. And the nine pairs of actual input-data (the nine boxy symbols) sit right upon the line of best fit, with no scatter, because R-squared = 1.00.
6b. Perfect Correlation without Perfect Proportionality (MX+C Model)
In Figure 5-B, we illustrated perfect proportionality between the entire MortRate and PhysPop (y = mx), as well as perfect correlation (R-Squared = 1.00).
By contrast, Figure 5-C illustrates perfect correlation between PhysPops and MortRates (R-squared = 1.00), but not perfect proportionality between the entire MortRates and their PhysPops. In order to see the proportionality between dose and response, one must first subtract the Constant from each MortRate, because the Constant represents a contribution to each MortRate which occurs "anyway" (even when dose = zero) and such a contribution is not proportional to dose.
6c. Can Perfect Correlation Persist, If X-Values Rise and Y-Values Fall?
The answer to the question in the subtitle is "Yes." To illustrate, we will do three linear regressions below. The first one reproduces the regression in Figure 5-C, so that we begin with "old" values (for x and y) which already have demonstrated their perfect correlation. In the second regression, each x-value of the first regression has been multiplied by 1.4, but the y-values stay as they are in the first regression. In the third regression, the x-values stay as they are in the second regression, but each y-value is multiplied by 0.8. So, the third regression shows a perfect correlation persisting even after all the x-values rose by one factor (1.4) and all the y-values fell by another factor (0.8).
Old-x Old-y #1. Regression Output:
159.72 132.90 Constant 19.9974
161.55 134.20 Std Err of Y Est 0.0029
123.14 107.05 R Squared 1.0000
169.76 140.00 No. of Observations 9
133.36 114.27 Degrees of Freedom 7
119.89 104.75
103.94 93.47 X Coefficient(s) 0.7069
85.83 80.67 Std Err of Coef. 0.0000
100.74 91.21 Except for rounding, input and output
are the same as Figure 5-C.
new-x old-y #2. Regression Output:
223.61 132.90 Constant 19.9942
226.17 134.20 Std Err of Y Est 0.0031
172.40 107.05 R Squared 1.0000
237.66 140.00 No. of Observations 9
186.70 114.27 Degrees of Freedom 7
167.85 104.75
145.52 93.47 X Coefficient(s) 0.5049
120.16 80.67 Std Err of Coef. 0.0000
141.04 91.21 Note: X-values are 1.4 times x-values in #1.
Note: This X-Coef = (0.7069 from #1) divided by 1.4 = 0.5049
new-x new-y #3. Regression Output:
223.61 106.32 Constant 15.9953
226.17 107.36 Std Err of Y Est 0.0025
172.40 85.64 R Squared 1.0000
237.66 112.00 No. of Observations 9
186.70 91.42 Degrees of Freedom 7
167.85 83.80
145.52 74.78 X Coefficient(s) 0.4040
120.16 64.54 Std Err of Coef. 0.0000
141.04 72.97 Note: Y-values are 0.8 times y-values in #2.
Note: This X-Coef = (0.5049 from #2) * 0.8 = 0.4039
Note: This Constant = (19.9942 from #2) * 0.8 = 15.9954
* Part 7. Dose-Response: Effects of Imperfect Matching across Dose-Groups
For multi-cause diseases such as Cancer and Ischemic Heart Disease, we can define co-actors as necessary co-causes in producing single cases of those diseases (Introduction, Parts 4 and 5). When analysts want to study the dose-response between one co-actor (for instance, medical radiation) and the mortality rate from the disease, they hope to compare study-groups which differ in dosage of the one co-actor but which are alike ("matched") with respect to the other co-actors (for instance, smoking). In this book, the study-groups (or dose-groups) are the populations of the Nine Census Divisions.
7a. The Real World: Imperfect Matching across Dose-Groups
In the real world of cancer-studies, perfect matching across dose-groups is never possible. Practical obstacles are immense. In addition, all causes of Cancer are probably not even recognized yet, and it would be impossible to match dose-groups for unrecognized co-actors. For both reasons, imperfect matching always occurs.
Imperfect matching for co-actors can interfere with detection of a positive correlation which is truly present, or can produce an apparent correlation which is spurious. The power of "confounding variables" is a major concern for all analysts. In this book, we need not worry about finding a spurious positive correlation (between medical radiation and cancer MortRates), because a causal relationship between ionizing radiation and fatal Cancer has been well established by a multitude of earlier studies (Chapter 2, Part 4c). But we need to appreciate the power of imperfect matching to obscure the correlation in a set of data.
7b. Figure 5-D: Inconsistency with the "Correlation Axiom"
Comparison of Figures 5-B and 5-D, at the end of this chapter, illustrates how imperfect matching for co-actors can change a perfect correlation (R-Squared = 1.00) into an imperfect correlation with an R-Squared value of 0.7112.
Figure 5-D uses the real 1940 PhysPops as the x-values, as did Figure 5-B. However, Figure 5-D depicts the consequence of Census Divisions which are imperfectly matched for co-actors. The unequal average exposure to nonradiation co-actors, in the Nine Census Divisions, can degrade the PhysPop-MortRate correlation in two ways. One: Xray potency per rad is modulated differently in the various Census Divisions (Chapter 6, Part 6; and Chapter 49, Part 2). Two: The number of cases in which xrays are not a co-actor may differ across the Census Divisions. As a result of one or both phenomena, the MortRates from Figure 5-B increase by irregular numbers (purely illustrative) as follows:
MortRate Increments in MortRate due to
Fig.5-B Imperfect Matching of Co-Actors
"y" in Figure 5-D
Pacific Division: 112.9029 + 25 = 137.9029
New England: 114.1965 + 11 = 125.1965
West North Central: 87.0452 + 20 = 107.0452
Mid-Atlantic: 120.0000 + 17 = 137.0000
East North Central: 94.2696 + 35 = 129.2696
Mountain: 84.7479 + 11 = 95.7479
West South Central: 73.4731 + 21 = 94.4731
East South Central: 60.6715 + 45 = 105.6715
South Atlantic: 71.2111 + 31 = 102.2111
As a result of imperfect matching, the R-squared value of 1.00 in Figure 5-B falls to 0.7112 in Figure 5-D. The true biological correlation is obscured (but not changed) by imperfect matching of co-actors across the dose-groups. Imperfect matching is not consistent with what we can abbreviate as the "Correlation Axiom," below.
The Correlation Axiom
Correlation Axiom: Increment in cancer MortRate is perfectly proportional to increment in radiation dose (PhysPop), provided that co-actors are perfectly matched across the dose-groups. The Correlation Axiom describes (a) the linear dose-response, and (b) the matching of dose-groups --- which is a fundamental principle of dose-response research, even though it is never fully achievable (Part 7a; also Chapter 3, Part 2d).
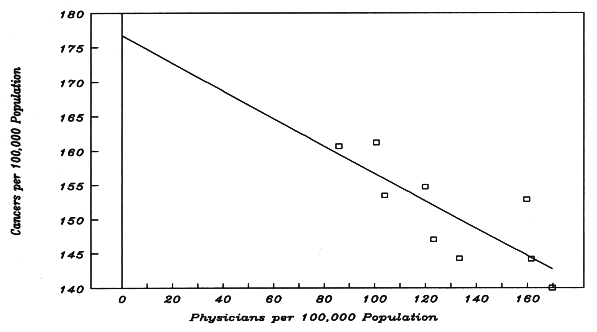
7c. Figure 5-E: A Truly Positive Correlation Which Looks Negative
Imperfect matching for co-actors can interfere --- much more severely than illustrated in Figure 5-D --- with detection of a positive correlation which is truly present. With Figure 5-E, we will demonstrate how imperfect matching can even make a truly positive correlation appear negative.
We are preparing to study the dose-response between PhysPop (surrogate for medical radiation) and cancer MortRates. Suppose that a carcinogenic co-actor, such as smoking, occurs with the most intensity where PhysPop values are the lowest, and with the least intensity where PhysPop values are the highest. In other words, suppose there is an inverse relationship between PhysPop and smoking. In such a situation, smoking will increase the cancer MortRates more in Census Divisions with low PhysPop values than in Census Divisions with high PhysPop values. Below, starting with the values from Figure 5-B, we arrange the Census Divisions in descending order of their 1940 PhysPop values, and then we add to the 1940 cancer MortRates from Figure 5-B in a way inverse to the trend of PhysPop values:
1940 MortRate Increments in MortRate due to
PhysPop Fig.5-B Imperfect Matching of Co-Actors
"y" Fig.5-E Regression Output:
Mid-Atl 169.76 120.0 + 20 = 140.0 Constant 176.7119
New Eng 161.55 114.2 + 30 = 144.2 Std Err of Y Est 4.8615
Pacific 159.72 112.9 + 40 = 152.9 R Squared 0.6322
ENoCen 133.36 94.3 + 50 = 144.3 No. of Observations 9
WNoCen 123.14 87.0 + 60 = 147.0 Degrees of Freedom 7
Mtn 119.89 84.7 + 70 = 154.7
WSoCen 103.94 73.5 + 80 = 153.5 X Coefficient(s) -0.2003
SoAtlan 100.74 71.2 + 90 = 161.2 Std Err of Coef. 0.0577
ESoCen 85.83 60.7 + 100 = 160.7 X-Coef / S.E. = -3.4686
The regression-output in Figure 5-E shows that the sign on the X-Coefficient has become 0.20 with a negative sign, which means that when PhysPop increases by one unit, cancer MortRate falls by 0.2 unit. In other words, the true positive correlation between PhysPop and cancer MortRate has been so well concealed by the non-matched co-factor (smoking), that the observed correlation between PhysPop and cancer MortRates will be inverse in such a situation. But imperfect matching of co-actors is just an error, an inconsistency with the Correlation Axiom. Such errors have no power to repeal the laws of physics and human biology --- the laws which established the Correlation Axiom for ionizing radiation (PhysPop) in the first place.
* Part 8. Real-World "Entropic Circumstances" Which Reduce Observed Correlations
The ideal MX model and the ideal MX+C model both reflect perfect correlation between dose and response. They are very orderly models. But in the real world, order is opposed by the tendency toward disorder. Most systems move spontaneously from states of order toward states of disorder. In chemistry, the molecular chaos of a substance or a system is measured by a property called "entropy."
What Do We Mean in This Book by "Entropic Circumstances"?
In this book, we need a name for the group of real-world events which perturb the orderly, ideal models of this chapter. Our name is "entropic circumstances." Entropic circumstances operate generally against order --- they do not create order. (Weiss 1998 describes some recent insights about entropy.)
8a. Some Specific Entropic Circumstances of Concern
For our dose-response studies, we know that two entropic circumstances of great concern have to be migration of populations from one Census Division to another (discussion in Chapter 3, Part 2c), and PhysPop deviations from "lockstep" over time (discussion in Chapter 3, Parts 2c and 8).
Both migration and deviations from PhysPop "lockstep" degrade PhysPops as surrogates for accumulated radiation dose-differences from medical applications. Neither migration nor deviations from PhysPop "lockstep" would be serious problems in our dose-response studies if complete delivery of radiation-induced cancers occurred within 2 or 3 years. They become problems because of the very gradual delivery-times for radiation-induced cancers --- with such delivery-times stretching over at least 40 years (or longer) for mixed-age populations. By comparison, other entropic circumstances may be less important --- and we emphasize "may."
8b. Finding the Maximum Real-World Correlations (PPs with MRs)
Because entropic circumstances operate against orderly phenomena (such as correlations), entropic circumstances reduce R-Squared values. Therefore, if we seek the best approximation of the real dose-response relationship, between PhysPops and cancer MortRates, we will seek and accept the highest values of R-squared which survive erosion by entropic circumstances.
1940 is our first year of MortRate data with all 48 states represented. And 1921 is the year of our earliest PhysPop data. In our search for the strongest correlation, we regressed the 1940 MortRates serially on every set of prime (not interpolated) PhysPop data between 1921 and 1940 --- including the 1940 PhysPops. Although cancer mortality during 1940 can hardly be influenced by medical radiation received during 1940, the 1940 PhysPops are nearly in "lockstep" with the PhysPops of many preceding years (Chapter 3, Table 3-C) --- and thus, 1940 PhysPops reflect the approximate differences in accumulated dose of medical radiation from many prior years.
* Part 9. Estimating the Impact of Medical Radiation on Cancer MortRates
We undertook this project in order to explore Hypothesis-1, that medical irradiation is the principal cause of cancer mortality in the USA during the Twentieth Century. We remind readers that we are not trying to establish the existence of a positive correlation between ionizing radiation and cancer mortality. That was proven many years ago. Instead, we are making use of that knowledge to test Hypothesis-1.
We begin, in Section Two of this book, by looking at what we can learn about Hypothesis-1 from regressing 1940 cancer MortRates on earlier PhysPops. In Section Five of this book, we examine the whole 1940-1990 period. We arrive at estimated Fractional Causation of cancer mortality by medical radiation. Such results clearly support Hypothesis-1.
Figure 5-A. Annual Delivery-Rates of Radiation-Induced Cancer Related Text = Parts 1, 2, + 3.
o - Each box in the grid represents 3 cases of radiation-induced cancer per 100,000 population (mixed ages).
o - Each horizontal row of 40 boxes represents gradual delivery of 120 cancers per 100,000 population. In this illustration, 120 is the number of cases produced by the radiation received during a single calendar-year. These 120 cases are delivered gradually at the rate of 3 cases per year for 40 years.
o - Each vertical column represents the number of radiation-induced cancers delivered during a single calendar-year, per 100,000 population, from all earlier years of irradiation. All boxes in a column were produced by radiation received in different calendar-years.
o - Both shaded columns have 40 vertical boxes (representing 120 cancers) as do the columns between the two shaded columns. Such columns demonstrate the "Law of Equality": The annual radiation- induced delivery of 120 - the annual radiation-induced production of 120.

Figure 5-B. The MX Model of Dose-Response Related Text = Part 5.
Census Divisions 1940 1940 Best-Fit
"x" "y" Calc.
PhysPops MortRates MortRates
Pacific 159.72 112.9029 112.9029 Regression Output:
New England 161.55 114.1965 114.1965 Constant 0.00000
West No. Central 123.14 87.0452 87.0452 Std Err of Y Est 0.00000
Mid-Atlantic 169.76 120.0000 120.0000 R Squared 1.00000
East No. Central 133.36 94.2696 94.2696 No. of Observations 9
Mountain 119.89 84.7479 84.7479 Degrees of Freedom 7
West So. Central 103.94 73.4731 73.4731
East So. Central 85.83 60.6715 60.6715 X Coefficient(s) 0.706880
South Atlantic 100.74 71.2111 71.2111 Std Err of Coef. 0.000000
Additional PhysPops 90.00 63.6192
--- not "observed" --- 80.00 56.5504
down to zero PhysPop 70.00 49.4816
(zero medical 60.00 42.4128
radiation). For each, 50.00 35.3440
we calculate a best- 40.00 28.2752
fit MortRate. These 30.00 21.2064
additional x,y pairs 20.00 14.1376
are also part of the 10.00 7.0688
best-fit line. 0 0.0000
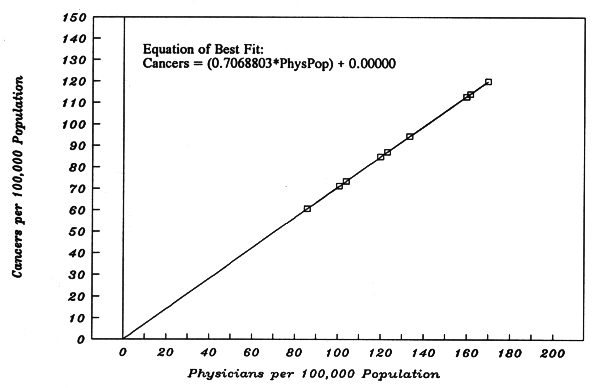
Figure 5-C. The MX+C Model of Dose-Response Related Text = Part 6a.
Census Divisions 1940 1940 Best-Fit
"x" "y" Calc.
PhysPops MortRates MortRates
Pacific 159.72 132.9029 132.9029 Regression Output:
New England 161.55 134.1965 134.1965 Constant 20.0000
West No. Central 123.14 107.0452 107.0452 Std Err of Y Est 0.0000
Mid-Atlantic 169.76 140.0000 140.0000 R Squared 1.000000
East No. Central 133.36 114.2696 114.2696 No. of Observations 9
Mountain 119.89 104.7479 104.7479 Degrees of Freedom 7
West So. Central 103.94 93.4731 93.4731
East So. Central 85.83 80.6715 80.6715 X Coefficient(s) 0.706880
South Atlantic 100.74 91.2111 91.2111 Std Err of Coef. 0.000000
Additional PhysPops 90.00 83.6192
--- not "observed" --- 80.00 76.5504
down to zero PhysPop 70.00 69.4816
(zero medical 60.00 62.4128
radiation). For each, 50.00 55.3440
we calculate a best- 40.00 48.2752
fit MortRate. These 30.00 41.2064
additional x,y pairs 20.00 34.1376
are also part of the 10.00 27.0688
best-fit line. 0 20.0000
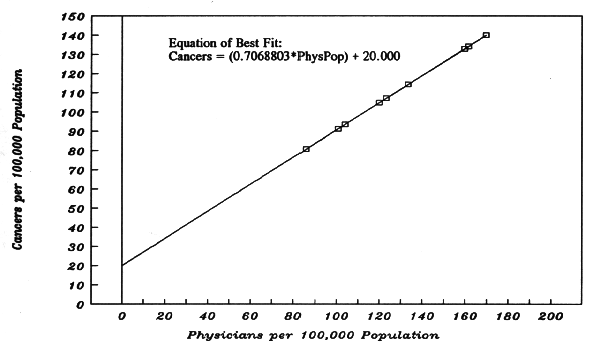
Figure 5-D. Effect of Imperfect Matching of Dose-Groups Related Text = Part 7b.
o Regression input for the x-variable (PhysPop) is the same as in Figure 5-B.
o Regression input for the y-variable (MortRate) comes from the text of Chapter 5, Part 7b. The MortRates differ from Figure 5-B in a manner which reflects Census Divisions which are imperfectly matched for radiation's carcinogenic co-actors.
o Each Best-Fit MortRate (to make the graph) is calculated with the equation of best fit provided by the regression output: MortRate = (0.4929 * PhysPop) + 51.5299.
Census Divisions 1940 Part 7b Best-Fit
"x" "y" Calc.
PhysPops MortRates MortRates
Pacific 159.72 137.9 130.3 Regression Output:
New England 161.55 125.2 131.2 Constant 51.5299
West No. Central 123.14 107.0 112.2 Std Err of Y Est 9.9955
Mid-Adantic 169.76 137.0 135.2 R Squared 0.7112
East No. Central 133.36 129.3 117.3 No. of Observations 9
Mountain 119.89 95.7 110.6 Degrees of Freedom 7
West So. Central 103.94 94.5 102.8
East So. Central 85.83 105.7 93.8 X Coefficient(s) 0.4929
South Atlantic 100.74 102.2 101.2 Std Err of Coef. 0.1187
Additional PhysPops 70.00 86.0 XCoef/SE 4.1523
--- not "observed" --- 60.00 81.1
down to zero PhysPop 50.00 76.2
(zero medical 40.00 71.2
radiation). For each, 30.00 66.3
we calculate a best- 20.00 61.4
fit MortRate. These 10.00 56.5
additional x,y pairs 0 51.5
are also part of the
best-fit line.
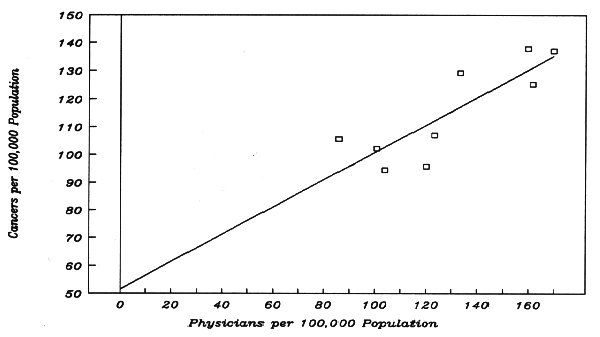
Figure 5-E. Effect of an Inverse Relationship between Dose and a Co-Actor Related Text = Part 7c.
o Regression input for the x-variable, (PhysPop) is the same as in Figure 5-B. The sequence here is in order of descending values. (Sequence does not affect regression output.)
o Regression input for the y-variable (MortRate) comes from the text of Chapter 5, Part 7c. The MortRates differ from Figure 5-B in a manner which reflects an inverse relationship between PhysPop and intensity of a co-actor across the Census Divisions.
Census Divisions 1940 Part 7b Best-Fit
"x" "y" Calc.
PhysPops MortRates MortRates
Mid-Atlantic 169.76 140.0 142.7 Regression Output:
New England 161.55 144.2 144.4 Constant 176.7119
Pacific 159.72 152.9 144.7 Std Err of Y Est 4.8615
East No. Central 133.36 144.3 150.0 R Squared 0.6322
West No. Central 123.14 147.0 152.0 No. of Observations 9
Mountain 119.89 154.7 152.7 Degrees of Freedom 7
West So. Central 103.94 153.5 155.9
South Atlantic 100.74 161.2 156.5 X Coefficient(s) -0.2003
East So. Central 85.83 160.7 159.5 Std Err of Coef. 0.0577
Additional PhysPops 70.00 162.7 X-Coef S.E. -3.4686
--- not "observed" --- 60.00 164.7
down to zero PhysPop 50.00 166.7
(zero medical 40.00 168.7
radiation). For each, 30.00 170.7
we calculate a best- 20.00 172.7
-fit MortRate. These 10.00 174.7
additional x,y pairs 0 176.7
are also part of the
best-fit line.