ABSTRACT
The analytical model of nuclear reactor transients, incorporating both mechanical and nuclear effects, simulates reactor kinetics. Linear analysis shows the stability borderline for small power perturbations. In a stable system, initial power disturbances die out with time. With an unstable combination of nuclear and mechanical characteristics, initial disturbances persist, and may increase with time. With large instability, oscillations of great magnitude occur.
Stability requirements set limits on the power density at which particular reactors can operate. The limiting power density depends largely on the product of two terms: the fraction of delayed neutrons and the frictional damping of vibratory motion in reactor core components. As the fraction of delayed neutrons is essentially fixed, mechanical damping largely determines the maximum power density.
A computer program, based on the analytical model, calculates and plots reactor power as a non-linear function of time in response to assigned values of mechanical and nuclear characteristics.
A model, based on mathematical equations describing the nuclear and mechanical characteristics of reactors, simulates the transient response of reactor power. The nuclear and mechanical equations are tied by terms describing the heating effect of power transients, which distort the reactor structure, and in turn affect the power level. The combined mechanical and nuclear dynamics determine conditions for reactor stability.
THE MATHEMATICS OF REACTOR KINETICS
The analysis is based on two equations, one nuclear, the other mechanical. The nuclear equation relates the fractional power change to (1) the damping effect of delayed neutrons, and (2) the restoring effect of reactivity coefficients for temperature and density changes. The mechanical equation contains terms for (3) inertial resistance to acceleration, (4) mechanical damping of motion, (5) elastic resistance to distortion, and (6) thermal expansion of material caused by energy absorption.
The Nuclear EquationWe consider a "point" reactor[1],[2],[3], with time the only independent variable. Parameters describing the point reactor must be determined experimentally, or from equations dependent on spatial variables and neutron energy levels as well as time.
We assume that the average delay of fission neutrons is long compared to the period of power oscillations, so that the quantity of delayed neutrons produced during a transient depends on the neutron density accompanying the steady power level,
, which existed before the transient disturbance started.
With a negative temperature coefficient, a T, and a density coefficient of reactivity, a y, where y is the fractional change in density, the reactivity, r , is expressed,
r = r0 + aT T + ay y (1) The rate of change of power is then
dP/dT =[(aT T+ay y-b+r0 )P+P0 ]/ l (2) where b is the fraction of delayed neutrons and l is the average generation time of fission neutrons. A transient rise in the power level heats reactor material in accord with the first law of thermodynamics,
P-P0 = S dT/dt (3) where S = cp M is the heat capacity per unit temperature rise, cp is the specific heat at constant pressure and M is the heated mass of reactor material.
Combining Equations (2) and (3) to eliminate the temperature terms gives
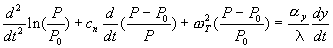
(4)
cn = b/l , w2T = - aT P0 /(S l) (5) and wT has the dimensions of inverse time, representing the natural frequency of a small power oscillation associated with the restoring effect of the negative temperature coefficient of reactivity.
Equations (1) to (5) have been developed and studied by other authors, including Thompson and Rodgers[1] and Weinberg and Wigner[2] (without the density term).
The last term in Equation (4), containing the density term, y, couples a rapid power transient to the mechanical dynamics of the reactor. A similar coupling is noted by Hetrick[4], who reports that the inertial effect increases the total energy produced during a transient.
The Mechanical Equation[5]Rapidly deformed reactor structures form a mechanical dynamic system, characterized by one or more fundamental or harmonic natural frequencies at which reactor parts may vibrate in response to external stimuli or to internal instabilities.
Any transient disturbance in material density or in the distribution of strains in certain parts or all of a heated reactor structure may affect the reactivity. Such a part of a particular reactor might be a vibrating fuel assembly, or moderator, or coolant. Non-uniform heating bends fuel elements away from a straight line. Heated moderators and reflectors expand, increasing leakage of neutrons from the reactor. Vapor cavities may form within reactor liquids, increasing or decreasing reactivity.
Large vibratory changes can lead to "fatigue" failure, and therefore are not generally acceptable in the design of permanent structures. Small disturbances in density or strain are considered in this analysis.
The partial differential equation for a mechanical vibration is divided by "separation of variables"[5] into ordinary differential equations, one dependent on time and one or more dependent on space. For solving the time equation, it often suffices to know the frequency of the system, without the details of the spatial distribution. The equation describing the vibratory motion of a heated material becomes,
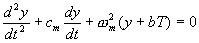
(6) where cm is the mechanical damping coefficient, and w m is the mechanical natural frequency of a reactor component whose motion changes reactivity. b is the coefficient of thermal expansion of the heated material.
Of the four terms in Equation (6), the first three appear in the conventional equation for the damped oscillation of a mechanical system.[5],[6] The first represents the force needed to overcome inertia, the second to overcome friction, and the third an elastic, or spring, force. The fourth term in Equation (6) is a forcing function. It represents the force accompanying the thermal strain caused by rapid changes in temperature, T.
Equations (4), (5) and (6) are a system for transients in reactor power, P, temperature, T, and density, y. Eliminating temperature and density terms yields a fourth-order differential equation with power as the dependent variable. The result is
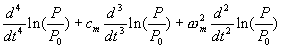
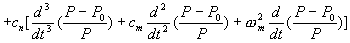
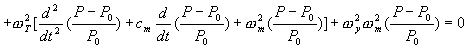
(7)
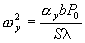
(8) and wy has the dimensions of inverse time. It represents a nuclear frequency dependent on the density coefficient of reactivity.
An equation essentially the same as Equation (7) was developed by Thompson[7]. An equation considering heat transfer delays, but without mechanical effects, was developed by Thompson and Rodgers[1].
Equation (7) is nonlinear because of the logarithm of power in the first three terms and the inverted power ratio in the next three terms. Its solution requires the use of finite difference equations and successive approximation procedures.
STABILITY OF EQUATION (7)The stability of a linear system, operating at or near equilibrium is a necessary, but not a sufficient, condition for stability under large ,non-linear departures from equilibrium. When only the temperature coefficient of reactivity,
, is considered, with no density coefficient,
, Equation (7) reduces to a second-order differential equation, always stable against small oscillations if its coefficients are positive.
The methods of linear transients pose two stability requirements for the linearized form of Equation (7). First, all coefficients must be positive. Second, the coefficients must satisfy Routh's criterion[8], namely,
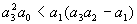
From Equation (7), the coefficients are
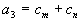
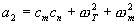
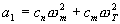
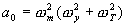
Replacing the
's with their values gives the stability requirement for Equation (7),
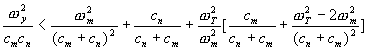
(9) For the combined nuclear and mechanical system, Equation (9) determines linear stability. The last term involving
has only a secondary effect on stability.
Particular values of two ratios of the variables in Equation (9) serve as reference points. For
the damping for an independent mechanical system is critical; above that value sustained oscillations cannot exist. Similarly, for
, where
is defined by
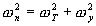
the independent nuclear system is critically damped, precluding sustained power oscillations. For most reactors nuclear damping is above the critical value, the right side of the inequality in Equation (9) is close to unity, and the expression for stability simplifies to
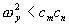
(10)
THE COMPUTER PROGRAMThe computer program solves Equation (7) by finite difference methods, using trial-and-error procedures to handle the highly non-linear equations. The program, in ZBasic[9] for an IBM-compatible personal computer, is available from the authors.
ESTIMATED VALUES OF THE COEFFICIENTSThe coefficients in the kinetic equation depend not only on materials, but also on specific reactor configuration. Let us develop possible values, based only on the properties of materials, and perhaps wide of the mark.
In Equation (7), the ratio,
, measures the rate of temperature rise in material heated by continuing steady-state power if the cooling system failed. An extreme high value may be 100 OC per sec, the lowest possible value being zero. The generation time,
, for fission neutrons may vary from 10-4 seconds for a thermal reactor to 10-7 seconds for a fast reactor. The negative temperature coefficient,
, (or positive density coefficient,
) may vary from zero (or even reverse sign) to 10-3 per OC. These figures would put the value of the nuclear frequency in the range, 0 <
< 1000 radians per second.
The neutron damping ratio is defined,
. The fraction of delayed neutrons for uranium is about = .007. The neutron damping ratio is considerably greater than the critical damping ratio,
.
The mechanical frequencies and the mechanical damping of parts of the reactor structure depend on the specific design.
CONCLUSIONSFor reactor conditions not satisfying the inequality of Equation (9), self-excited oscillations of power, temperature and density may occur. For stability both mechanical and neutron damping are necessary. Equation (10) appears to prescribe an upper limit to stable operating power density. Substituting the values for cn and y gives the requirement,
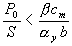
(11) Neutron generation time has disappeared from this expression. Increasing reactor power above incipient instability results in ever increasing severity of persistent oscillations.
DEFINITIONS
a0, a1, a2, a3 = coefficients in characteristic equation b = volume coefficient of thermal expansion, /oC cm = coefficient of mechanical damping, /sec cn = coefficient of neutron damping, b / l, /sec cp = specific heat at constant pressure, cal/gram-OC l = average generation time of neutron production, sec M = mass of heated materials, gram n = dimensionless time, wmt P = instantaneous power level, cal/sec Po = average power level, cal/sec S = heat capacity per unit temperature, cp M, cal/OC t = time, sec T = perturbation in temperature, OC TF = temperature, after cooling failure for time, t = p /w m y = perturbation on average density, dimensionless a y = density coefficient of reactivity, dimensionless a T = (negative) temperature coefficient of reactivity, /OC b = fraction of delayed neutrons r = reactivity, dimensionless w m = mechanical frequency, /sec w n = nuclear frequency =(w2y+ w2T)0.5 wT = nuclear frequency based upon temperature coefficient
of reactivity, w 2T = aTP0 /(S l), /secwy = nuclear frequency based upon density coefficient of
reactivity, w2y = ay bP0 /(S l), /sec
Definitions for Use in Examples:
A = time interval used in integration B = time at end of calculation run C = ratio, nuclear and mechanical frequency, wy/wm D = ratio, nuclear and mechanical frequency, wT/wm E = ratio, mechanical damping to mechanical frequency, cm /wm F = ratio, neutron damping to nuclear frequency, cn/wn G = initial excess reactivity, r0 /(wnl) H = initial power displacement, P1 /P0
COMMENTReactor proponents now promise us a new generation of inherently safe reactors based primarily on built-in physical characteristics, primarily a large negative temperature coefficient of reactivity. Equation (11) for the requirement for stability can be arranged,
-dr0/dt < b cm (12) where the term on the left is the rate of reduction in reactivity which would occur if the cooling system suddenly failed. It appears that the mechanical friction available in moving reactor parts may set a different stability limit. A given required amount of (positive) mechanical friction is notoriously difficult to assure in the presence of rapidly flowing cooling fluids.
REFERENCESThompson and Rodgers, Thermal Power from Nuclear Reactors, John Wiley & Sons, Inc., 1956, p. 116. Weinberg and Wigner, The Physical Theory of Neutron Chain Reactors, The University of Chicago Press, 1958, pp 603-609. Glasstone and Sesonske, Nuclear Reactor Engineering, Van Nostrand Reinhold Company, Chicago, 1967. David L. Hetrick, Dynamics of Nuclear Reactors, University of Chicago Press, Chicago, 1971. S. Timoshenko and D. H. Young, Vibration Problems in Engineering, D. Van Nostrand Company, Inc., Princeton, NJ, 1955, pp. 299, 409, 416. J. P. Den Hartog, Mechanical Vibrations, McGraw-Hill Book Company, Inc., New York, 1940, Ch. 7, p. 300. A. Stanley Thompson, "Study of Reactor Kinetics," American Society of Mechanical Engineers, Paper No. 62-WA-218, 1962. Chestnut and Mayer, Servomechanisms and Regulating System Design, John Wiley & Sons, Inc., New York, 1951. Andrew R. Gariepy, ZBasic Interactive BASIC Compiler, ZEDCOR, INC., Tucson, Arizona, 1987.