This chapter is arranged in seven parts:
-
Introduction, p.1
The Unmodified LQ Model, As Used by Radiation Committees,
p.2
The Modified LQ Model, As Described by Radiation Committees,
p.4
The Modified LQ Model, Fitting Supra-Linear, Linear, Sigmoid,
and Other Shapes, p.5
Proper Risk-Estimates for Low Acute Exposures,
p.9
Risk-Estimates for Slow Delivery of High Total Doses,
p.10
Risk-Estimates for Slow Delivery of Low Total Doses,
p.13
Then tables.
Then figures.
1. Introduction
If a cherished hypothesis comes into apparent conflict with valid human epidemiological evidence -- and note the term, "valid" -- then we clearly do not throw away valid evidence and insist on the hypothesis. The proper approach is to find out how and why such a hypothesis is inadequate to explain the valid epidemiological evidence.
Risk-Estimates for Low Acute Doses :
As shown in the previous chapter, those who support the existence of risk reduction-factors for acute low-dose exposures -- in the presence of human evidence against such factors -- commonly invoke "radiobiological considerations" as the justification.
Radiobiological considerations include the hypothesis that both intra-track and inter-track events can result in fully competent carcinogenic lesions, and that in a linear-quadratic (LQ) equation, the linear term represents intra-track carcinogenesis and the quadratic term represents inter-track carcinogenesis (see Chapter 19, Part 4). Thus, the sign should be positive for both the linear (L) and quadratic (Q) terms, and dose-response should be concave-upward.
Even if one accepts this hypothesis, the hypothesis can be readily reconciled with the real-world observation that, for carcinogenesis in the A-Bomb Study, human dose-response is supra-linear and concave-downward throughout the dose-range.
The reconciliation is achieved by modifying the LQ equation with an exponential modifier which represents a cell-inactivation function operating throughout the entire dose-range. By inactivation, we do not necessarily mean cell-killing, as we will explain in Part 4.
Recognition that the concave-upward shape, of an unmodified LQ equation, can be changed by an exponential modifier is nothing new. It has been recognized for decades. In fact, the format which we shall use in this chapter was displayed by NCRP in 1980 (Ncrp80, p.19) and by UNSCEAR-86 (p.188).
NCRP and all of the radiation committees recognized that an unmodified LQ equation was inherently false for human dose-response, when they all acknowledged that the curve flattens out "at high doses." Ncrp80 (p.160) even conceded that the supra-linear curvature was seen "at relatively low doses in the Hiroshima data." Various reports and analysts have explored use of "cell-killing" terms to modify their LQ equations -- but only to change their curvature at very high doses.
Since we all agree that the unmodified LQ equation does not match human dose-response, the task which remains is to modify an LQ equation so that it has what the human evidence requires: A supra-linear or a linear dose-response throughout the dose-range. If this can be done -- with both the L and Q terms positive -- of course it means that "radiobiological reasons" do not always predict a concave-upward dose-response at all.
It can be done, as this chapter demonstrates to any doubters.
Risk-Estimates for Slow Exposures :
Then, in Parts 6 and 7, we shall turn to the possible implications for dose-rate.
It is possible (though not certain) that a high acute dose is more carcinogenic than the same dose delivered slowly. We shall explore a range of possible values.
However, there is no reason at low total doses to expect more than trivial protection (reduction in risk) from slow delivery. ICRP itself acknowledged this, as noted in our Chapter 22, Part 3. In Part 7 of the present chapter, we have evaluated the maximum amount of protection which might occur if 5 rads, for instance, were given slowly instead of acutely. The amount would be very small indeed.
Therefore, the low-dose Cancer-Yields in Section 4 of this book are definitely valid for slow delivery as well as for acute delivery.
2. The Unmodified LQ Model,
As Used by Radiation Committees
For the unmodified LQ model, depicted in Figures 23-B and 23-C, we use the following notation:
A cancers = intra-track cancers.
B cancers = inter-track cancers.
(A+B) cancers = total excess cancers.
D^1 = dose in cSv to the first power.
D^2 = dose in cSv squared.
(a cancers per cSv) = coefficient of the L term.
(b cancers per cSv^2) = coefficient of the Q term.
-
The units cancel out when we write:
A cancers = (a cancers cSv^-1) x (D^1 cSv^1)
A = aD^1
B cancers = (b cancers cSv^-2) x (D^2 cSv^2)
B = bD^2
In the radiation literature, one sees suggestions that the linear and quadratic terms may make equal contributions to total excess cancer (radiation-induced cancer) at doses between 50 and 150 rads (cGy). These are purely speculative limits. We shall explore limits of 50 and 400 cSv.
A = B at 50 cSv :
If A = B at 50 cSv, we would write from Equations (1) and (2):
(a cancers cSv^-1) x (50 cSv) =
50a = 2500b
a = 50b.
This is a ratio (a/b = 50), and we can set the value of b equal to 1.0 for the sake of clarity in producing Table 23-B.
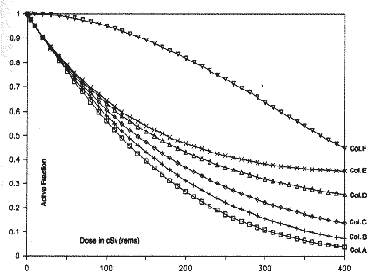
Table 23-B shows the values of A, B, and (A+B) when b = 1.0, if A = B at 50 cSv. Because we have shown (above) that a = 50b in these circumstances, we can substitute (50b) for (a) in the equation A = aD^1. Thus the entries for Column A in Table 23-B are calculated from the equation A = (50b)(D^1).
In the row for 50 cSv, readers will find equal cancer-contributions from the intra-track and inter-track terms: 2,500 from each.
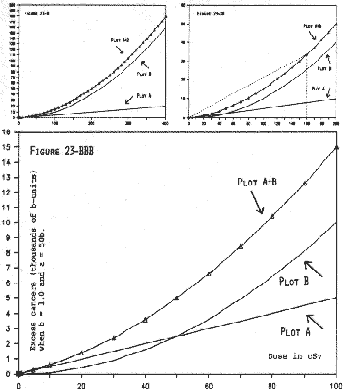
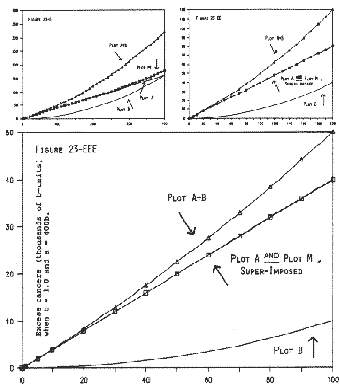
From Table 23-B, Columns A, B, and (A+B) are depicted by Figure 23-B, BB, BBB. This is a single figure in which 23-B examines the plots out to 400 cSv, 23-BB examines them out to 200 cSv, and 23-BBB examines them out to 100 cSv. In Figure 23-BBB, it is clear that A = B at 50 cSv. This is visible also in Figure 23-BB.
A = B at 400 cSv :
If A = B at 400 cSv, we would write a = 400b. Table 23-C shows the values of A, B, and (A+B) when b = 1.0, if A = B at 400 cSv. In the row for 400 cSv, readers will find equal cancer-contributions from A and from B: 160,000 from each.
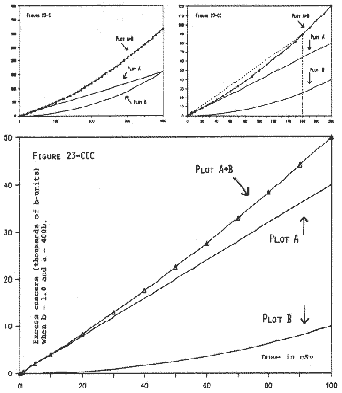
From Table 23-C, Columns A, B, and (A+B) are depicted by Figure 23-C, CC, and CCC. Figure 23-C examines the plots out to 400 cSv, 23-CC examines them out to 200 cSv, and 23-CCC examines them out to 100 cSv. In Figure 23-C, it is clear that A = B at 400 cSv.
The Mistaken Risk-Reduction Factors for Acute Exposures :
It is self-evident from Figures 23-B and 23-C that the unmodified LQ model produces a concave-upward curvature for total excess cancers -- Plot (A+B). This matches the presumption discussed in Chapter 22. Indeed, Figure 23-BB closely resembles the model displayed by Ncrp80 (p.16, Figure 3.4). Comparison of Figures 23-B and 23-C also shows that the concave-upward curvature is much greater if A = B at 50 cSv than if A = B at 400 cSv.
We shall calculate risk reduction-factors for both limits, for acute exposures, as if dose-response were actually concave-upward. Let us assume that we have observation of risk-rates only at 160 cSv of acute exposure and at zero dose (in other words, two datapoints), and we decide to estimate the risk from acute exposure at very low doses, by making a linear interpolation between 160 cSv and zero dose.
On Figures 23-BB and 23-CC, we have drawn a dashed straight line from Plot A+B at 160 cSv (the high-dose observation) to the origin. This dashed line lies above the A+B curve at low doses, and so linear interpolation would overestimate risk at low doses -- if dose-response were truly concave-upward.
When the dose is very low, readers can see for themselves that Plot B (the quadratic term) generates about zero excess cancer. At low doses, essentially all the excess cancers are coming from intra-track carcinogenesis (Plot A). This is not in dispute. Indeed, the Figures show that Plot A+B and Plot A are just about on top of each other, and their slopes are about the same in the low dose-range.
DREFS -- The Ratio of Slopes :
Under these circumstances of interpolation, it would be appropriate for everyone to estimate risk reduction-factors by dividing one slope by another: The slope of Plot A+B shown as the dashed line between zero and 160 cSv, by the slope of Plot A -- because the slope of Plot A approximates the actual slope of Plot A+B at low doses. As stated in Chapter 22, Part 1, a DREF is the ratio of the steeper slope over the lower slope (Ncrp80, p.176). Since slope in these circumstances means excess cancers per cSv, the centi-sieverts cancel out in such a division, and the ratio of excess cancers remains.
If A = B at 50 cSv, the slope of the dashed line is 33600 / 160, or 210. The value 33600 need not be read off Figure 23-B; it comes from Table 23-B, the A+B column at 160 cSv. The slope of Plot A is 8000 / 160, or 50. The ratio of the slopes is 210 / 50, or 4.2. Therefore, if the plots shown in Figure 23-B were actually observed plots matching real-world data, linear interpolation from 160 cSv would overestimate risk at low doses by 4.2-fold. Under these circumstances, a risk reduction-factor of 4.2 would be appropriate.
If A = B at 400 cSv, the slope of the dashed line in Figure 23-CC is 89600 (from Table 23-C) divided by 160, or 560. The slope of Plot A is 64000 / 160, or 400. The risk reduction-factor under such circumstances would be 560 / 400, or 1.4-fold, to make interpolations from 160 cSv.
Visual comparison of Figure 23-BB with 23-CC shows why the presumption of A = B at 50 cSv "requires" a much larger risk reduction-factor than the presumption that A = B at 400 cSv, if linear interpolation is used. In Figure 23-BB, the linear term (Plot A) accounts for only a small share of Plot A+B. In Figure 23-CC, the linear term (Plot A) is not very distant from Plot A+B, and so linear interpolation from Plot A+B at 160 cSv "requires" less of a correction.
Nature of the Mistake :
We put "requires" in quotes because no risk reduction-factors are required for acute exposures at all, for two reasons: (1) dose-response in the human is not concave-upward, and (2) direct human observations at low doses leave no need to use high-dose data, in order to estimate low-dose risks.
The LQ Model -- Positive vs. Negative Q-Coefficient :
The underlying assumption of this model is that combined action of intra-track carcinogenesis and inter-track carcinogenesis gives rise to the total radiation-induced cancers (A+B). Therefore, both the linear and quadratic terms are presumed to be positive. It follows that at every dose, the points along Plot A+B are necessarily the sum of the corresponding points along Plot A and Plot B. If inter-track carcinogenesis is occurring at all, Plot A+B must always lie above Plot A. Moreover, the shape of Plot B guarantees that the shape of A+B is concave-upward.
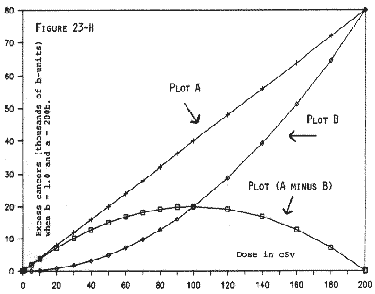
However, when analysts try to fit the LQ model to a supra-linear set of datapoints, regression analysis produces a best-fit equation in which the quadratic term is negative (see Chapters 14 and 22). This means that the points along the combined linear and quadratic plot are the A values minus the corresponding B values. The result is necessarily a supra-linear, concave-downward plot, as illustrated by Figure 23-H.
The findings that (1) the Q-term is negative and (2) the dose-response is concave-downward, do not require any presumption, however, that intra-track lesions are carcinogenic and inter-track lesions are protective. Such a hypothesis would be utterly implausible, as shown in Chapter 19, Part 4.
The concave-downward dose-response, which is observed in the evidence, is perfectly consistent with positive signs for both the linear and quadratic terms -- as we shall show in Part 4 of this chapter.
3. Modified LQ Model,
As Described by Radiation Committees
No one disputes that the concave-upward shape of an LQ model can be altered by adding an exponential modifier. Indeed, we will use the type of modifier suggested by Ncrp80 (p.19, Figure 3.5):
I = [aD^1 + bD^2] x [exp-(m'D^1 + m"D^2)]
where I = incidence of effect being studied (total excess cancers).
Equation (4) is clearly the unmodified Equation (3), except for the righthand term between brackets. The quantity between the righthand pair of brackets is the "exponential modifier" by which the quantity between the lefthand pair of brackets is multiplied. Some readers will want to review the meaning of "exp." See Chapter 19, Part 2, Poisson Equation, and the note below Table 23-A in this chapter. (We shall defer examination of Table 23-A, for its other purposes, until later.)
In Equation (4), the cSv-unit cancels out in the modifier, because the units of the m' and m" coefficients are cSv^-1 and cSv^-2, respectively.
Contribution of the NCRP :
Discussions of radiation carcinogenesis commonly refer to the necessity of modifying the LQ model, by some additional term, in order to fit the "leveling off" and "flattening" and "falling" of the incidence curve with rising dose. Almost invariably, these phenomena are described as occurring at high doses. For instance, Ncrp80 (p.17) states:
"The phenomenon of the dose-response curve leveling off and then falling at high doses ... is seen frequently in radiobiology and specifically in curves for mutagenesis and carcinogenesis. Its cause, although incompletely understood, is frequently ascribed to cell killing. Since it is still seen in cell transformation experiments in tissue culture in which the results are normalized to surviving cells ... it could be due at least in part to intracellular processes that prevent the presumed `induction' phenomenon from becoming manifest."
The NCRP statement above is very useful, and it is clear that NCRP does not consider cell-killing as necessarily the only explanation for the "leveling off" effect. We would agree on that point.
But we fault the NCRP statement for its general suggestion that the "leveling off" effect is necessarily a high-dose effect. The understanding of why radiobiology and epidemiology are not in conflict depends upon not pre-judging how intense the "leveling off" effect is and at what dose it becomes appreciable.
The NCRP formulation using an exponential term, in order to take account of the "leveling off" effect, is quite reasonable. But after introducing the expression [exp-(m'Dose^1 + m"Dose^2)], it is totally unreasonable to pre-judge what the appropriate values for m' and m" are going to be. (It might be noted that Ncrp80 uses the gamma and delta symbols instead of m' and m".)
The values of the m' and m" coefficients in the exponential term must be determined by curve-fitting with real data, not by some pre-judgment which can totally distort the reality of epidemiological evidence.
Pre-Judgment in NIH Report :
Other discussions in the literature, of the linear and quadratic terms, also tend to suggest that the "leveling off" effect can occur only at very high doses -- a suggestion which I am sure has added wholly unnecessary confusion to the scene.
For example, in the 1985 NIH Report, the authors refer to how various "official bodies" (their term) have handled risk-reduction factors, and in this discussion, they say (Nih85, p.26):
"The BEIR III Committee did not incorporate the competing effect of cell inactivation, mainly at high dose levels, into its risk calculations, although it did consider the problem theoretically ..." The NIH Report also states, in discussing the Japanese A-bomb survivors (p.26-27):
"Doses high enough to reduce the carcinogenic response appreciably through the competing effect of cell inactivation might well be in the lethal range for man when delivered to his whole body."
The NIH Report clearly takes an extremely prejudicial position on how very high the doses might have to be, before cell inactivation could influence the dose-response for cancer. The NIH committee has decided, contrary to the evidence available in 1985 from the A-Bomb Study, that whole-body doses might have to be high enough to be lethal to man.
Implications of Breast-Cancer Data :
Moreover, it would appear that the NIH committee did not consider the implications of its own acceptance of the conclusion that the dose-response for human breast-cancer is linear over the entire dose-range (Chapter 22, Part 2).
The acceptance of linearity at all doses implies either (1) inter-track carcinogenesis is negligible over the entire dose-range, or (2) the "leveling off" effect from cell inactivation is appreciable enough at low doses to off-set the concave-upward curve of Plot B. Indeed, where whole-body exposure occurred (the A-bomb survivors), the "leveling off" effect was appreciable enough to make the dose-response for breast-cancer concave-downward rather than linear (Ncrp80, p.144; Go81, Chaps. 10,11).
"Radiobiologic Findings" :
It is my opinion that pre-judgments or "blind-spots" about the interaction of the linear term, quadratic term, and the cell-inactivation term, have led to much nonsense about radiobiology being in conflict with human epidemiological evidence, and to suggestions that we must accept dose-response curves "based on radiobiology" even though the proposed curves are totally at variance with real human epidemiological data of good quality.
For instance, "radiobiologic findings" were named as the basis when BEIR-3 endorsed upward curvature (Beir80, p.261), and substituted a leukemia curve for the all-cancer curve; see our Chapter 22, Part 3. This substitution was noted by RERF analysts in explaining why their own risk-estimates are higher than BEIR-3's:
[Some of the disparity] " ... may be ascribed to the fact that in BEIR III, the curvature in dose response for leukemia was used for all cancers except leukemia instead of the actual curvature which probably is much closer to linearity, and this may cause much smaller estimates to be produced than if the actual dose-response curve were to be applied" (Shi88, p.51).
4. A Modified LQ Model,
Fitting Supra-Linear, Linear,
Sigmoid, and Other Dose-Responses
Unlike the radiation committees cited in Part 3, we shall not assume that the cell-inactivation term -- which is the exponential modifier in Equation (4) -- applies only at some arbitrarily high radiation dose. Instead, we shall investigate how this term can be used to fit actual human epidemiological data having supra-linear and linear dose-responses.
Moreover, we shall not pre-judge how prominent the linear term (A, or intra-track carcinogenesis) is in comparison with the quadratic term (B, or inter-track carcinogenesis). We shall explore two limits: A = B at 50 cSv, and A = B at 400 cSv.
When A = B at 50 cSv, the unmodified LQ dose-response has a markedly concave-upward curvature (Figure 23-B), but even such curvature becomes concave-downward with the appropriate cell-inactivation function -- as we shall show.
Cell-Inactivation, and Table 23-A :
To explain the observed "leveling off" of radiation carcinogenesis with rising dose, some analysts refer to the need for a "cell-killing" term. We do not regard cell-killing as the only possible explanation. Some other analysts make the presumption that "cell sterilization" occurs with rising dose, and that inability of cells to reproduce accounts for the observation. Also, it is possible that what accounts for the observation is redundancy of carcinogenic lesions, with rising dose, or dose-dependent changes in the biochemical milieu.
In the absence of evidence on the cause or causes of supra-linear and linear dose-responses, we prefer to use the term "cell-inactivation."
"Cell-inactivation" is a term compatible with all possibilities. It implies that, as dose rises, (1) a decreasing fraction of irradiated cells remains capable of providing the precursors of a clinical cancer, and (2) an increasing fraction of irradiated cells becomes "inactivated" with respect to developing into clinical cancers, even though radiation may have produced carcinogenic alteration in such cells.
It must be emphasized that there are no rules and no radiobiological principles which prevent variation of the cell-inactivation term, from one species to another. We shall return to this issue early in Part 5.
Table 23-A evaluates the cell inactivation term for various pairs of m' and m" values in Equation (4) -- which is the modified LQ model. For convenience, it is provided again below.
In Table 23-A, one finds that the "active" fraction is 100 % at zero dose, and falls with rising dose. Figure 23-A shows that the fractions fall in a non-linear manner.
A = B at 400 cSv.
Modified LQ Model Yields Supra-Linearity :
In Part 2, we showed how Table 23-C yields Figure 23-C -- a concave-upward dose-response with no "leveling off" or flattening at high doses. We plotted only the A, B, and A+B columns.
Now we return to Table 23-C, where A = B at 400 cSv, and we call attention to Column C. Column C shows dose-response (A+B) as modified by the cell-inactivation term when m' = 0.005 and m" = -0.000004. In other words, Column C is the evaluation of Equation (4) when those are the values of m' and m".
For instance, if we use 100 cSv as an example, the entry in Col. C is 50,000 excess cancers (from Column A+B, unmodified, at 100 cSv) times 0.63128 (the value of the cell inactivation term, from Table 23-A, Column D, at 100 cSv), or 31,564 excess cancers. The cell-inactivation term operates upon the intra-track and inter-track terms alike. One arrives at the same entry by modifying the A and B entries at 100 cSv separately: (40,000 x 0.63128) + (10,000 x 0.63128) = 31,564.
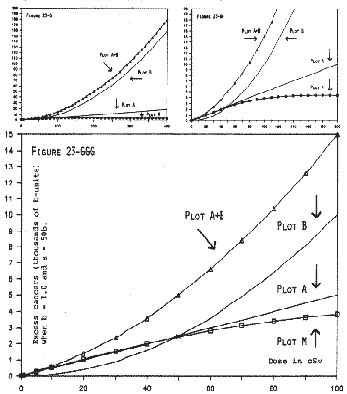
In Figure 23-D, we have plotted Column C as Plot M (for Modified). Otherwise, Figure 23-D is exactly the same as Figure 23-C.
It is self-evident, in Figure 23-D, DD, and DDD that Plot M has a supra-linear, concave-downward shape throughout the dose-range.
Figure 23-D and the A-Bomb Study :
Plot M of Figure 23-D, DD, DDD is in harmony with the human dose-response observed in the A-bomb survivors.
Examination of Figure 23-DDD shows that Plot M starts diverging from the unmodified LQ dose-response (which is Plot A+B) at very low doses. In other words, the cell-inactivation term is already operating below 30 cSv to produce a supra-linear bend which is appreciable and detectable. This is in accord with the curvature noted in Chapter 14 for the A-bomb survivors.
On the other hand, no one should expect perfect matching between Figure 23-D, DD, DDD and the dose-response depicted in Chapter 14. Figure 23-D is constrained only by its equation, whereas Figures 14-E and 14-F are constrained not only by different equations, but also by real-world datapoints. The plots in Chapter 14 are empirical best-fits to actual data, and thus do not pre-judge the interplay of factors such as possible population heterogeneity, possible lethargy of repair-systems at very low doses, possible effects of biochemical milieu, possible redundancy of injury, or other factors which may affect the steepness of slope in the very low dose-region.
A Spurious Conflict :
If we return to Figure 23-D, DD, DDD, the key point is that a modified LQ model resolves any alleged conflict between the real-world observation -- that supra-linearity (starting at very low doses) occurs throughout the entire dose-range of the A-Bomb Study -- and "radiobiology."
We cannot explain why the assumption is made, by so many, that the modifying term in an LQ model cannot operate below very high doses. There seems to be no logical or scientific basis for such an assumption. When we permit the modifying term in Equation (4) to have effect at quite low doses, we are not assaulting the LQ model. More importantly, we can attain a curve which is compatible with human epidemiology, instead of substituting a curve which assaults such evidence.
The Graphic Meaning of "Supra-Linear" and "Sub-Linear" :
Examination of Figure 23-DD shows clearly that Plot M has a concave-downward bend. If a straight line were to connect any two points along Plot M, the curve of Plot M would lie above the straight line. That is why it is correct to characterize a shape like Plot M as supra-linear.
If confusion is to be avoided, the standard for describing the shape of a curve must be the curve itself, and not some other curve which may happen to be present in the same figure. Thus, the fact that Plot M lies beneath the linear Plot A does not make it appropriate to call it "sub-linear" -- a term encountered in the NRC's 1985 report (Gilb85, p.II-102). If Plot A were not in our figure at all, it would be impossible to guess the meaning of "sub-linear." By contrast, the term supra-linear is unambiguous with respect to shape.
As noted repeatedly in this book, another term commonly used for the supra-linear shape is "concave-downward." Far less common is the term "upward convex" -- a term encountered in Sho86 (p.693).
A = B at 400 cSv.
Modified LQ Model Yields Linearity :
Next we will show that, with certain other values of m' and m" in the cell-inactivation term, the LQ model is also fully consistent with observing a linear dose-response in human epidemiological studies.
We turn attention to Table 23-C again, where the linear and quadratic terms contribute equally to radiation-induced cancer at 400 cSv.
Column D modifies the LQ equation by using the following values in the cell-inactivation term: m' = 0.0025, and m" = -0.0000025. The details are in Note 2 of that table.
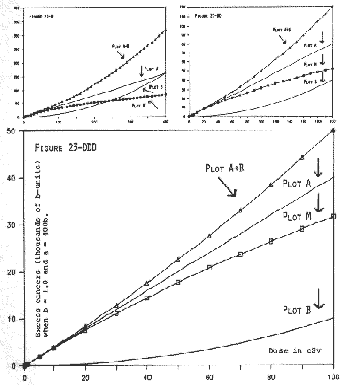
Column D is shown as Plot M (for Modified) in Figure 23-E. Except for Plot M, Figure 23-E is exactly the same as Figure 23-D.
It is self-evident, in Figure 23-E, that Plot M (the boxy symbol) looks linear from the origin out to about 250 cSv. Comparison of the entries in Table 23-C, Column A versus Column D, shows just how close the match is between the linear component (A) and the modified sum of A+B (Column D), out to 200 cSv. Indeed, Plot M is so very close to Plot A that one cannot distinguish the two plots from each other in Figure 23-EE, or EEE. In Figure 23-E, Plots A and M separate enough that, by about 250 cSv, we can discern that there are actually two plots, superimposed on each other, over most of the dose-range.
Thus, with a shift in the values of m' and m" in the cell-inactivation term, we can convert the concave-downward curve in Figure 23-D to a virtually perfect linear dose-response in Figure 23-E -- while the linear and quadratic terms are preserved intact.
Indeed, Figure 23-E shows that the effect of the exponential modifier (the cell-inactivation term), acting upon both the linear and quadratic terms, can produce a "pseudo-linear" result -- as if no quadratic term existed at all.
Linearity and Supra-Linearity --
Different Faces of the Same Coin ?
We pointed out at the end of Part 2 that, if there is a positive linear term and a positive quadratic term in radiation carcinogenesis, then, without modification, the sum of these two types of terms must necessarily give a concave-upward dose-response.
It follows that observation of a linear dose-response means that a cell-inactivation term (or some equivalent) must be operating to convert the concave-upward dose-response to linearity. In other words, observed linearity is a step on the way from concave-upward curvature to supra-linearity with just the intensity of the modification separating linearity from supra-linearity. Ncrp80 (p.18) also points out that linearity can be derived in this way, and that several workers have made this suggestion in the past.
Nonetheless, the insight has been ignored for almost a decade, while "radiobiology" was mistakenly invoked to support a concave-upward dose-response and the popular risk reduction-factors -- in the face of contrary human evidence.
Figures 23-D and 23-E reconcile radiobiology with reality. They are based on assuming a positive linear term, a positive quadratic term, and an exponential modifying term.
Next, we will show that the reconciliation is feasible also at the other limit -- when A = B at 50 cSv.
A = B at 50 cSv.
Modified LQ Model Yields Supra-Linearity
We now return to Table 23-B, where the linear term (A) and the quadratic term (B) are equally prominent at 50 cSv. The unmodified concave-upward shape of A+B was depicted in Figure 23-B.
We shall modify Column A+B of Table 23-B twice, as we did in Table 23-C. However, this time we shall illustrate conversion of Col. A+B into a sigmoid dose-response and then into a supra-linear dose-response.
Conversion to Sigmoid Shape :
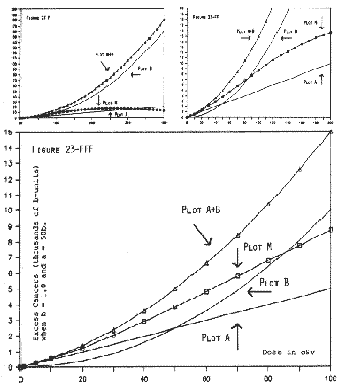
Column C from Table 23-B has been depicted as Plot M in Figure 23-F, FF, FFF. Otherwise, Figure 23-F and Figure 23-B are the same.
Figure 23-FF and FFF show that Plot M is concave-upward below 100 cSv. Since dose-response in the A-Bomb Study is not concave-upward in this dose-range, it is clear that the values of m' and m" tested by Column C are at variance with reality.
Nonetheless, Figure 23-F is provided here in order to help demonstrate that the method itself is not ruling out the sigmoid shape. We rule out the sigmoid shape on the basis of the human epidemiological evidence. The method itself is capable of fitting just about any dose-response one has ever seen. We shall return to this point.
Conversion to Supra-Linearity :
In order to convert Figure 23-F to supra-linearity, we need only to change the values of m' and m". This has been done in Table 23-B, Column D.
Column D from Table 23-B has been depicted as Plot M in Figure 23-G, GG, GGG. Except for Plot M, Figure 23-G and Figure 23-F are the same.
In Figure 23-GGG, the particular pair of values for m' and m" in Column D happens to make Plot M very nearly linear between 0 and 50 cSv. Beyond 50 cSv, Plot M becomes supra-linear.
It is evident, from Figure 23-GG, that Plot M (which is A+B modified) diverges from the unmodified Plot A+B at very low doses. Indeed, Figure 23-GGG shows that, by the time dose rises to 50 cSv, the cell-inactivation term has cut the excess cancer depicted by Plot M in about half, compared with the unmodified Plot A+B.
A = B at 100 cSv.
Additional Conversions of the LQ Model :
Readers need not depend on our assertion that the modified LQ model is capable of fitting a vast variety of observed dose-responses.
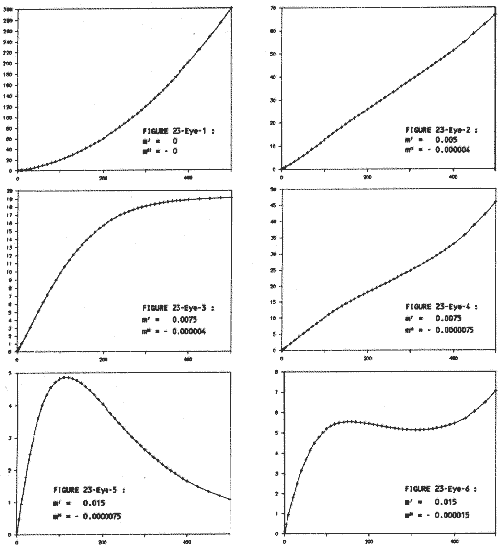
For instance, Figure 23-I (Eye) shows how merely changing the values of m' and m" converts the unmodified concave-upward model (where m' = 0, and m" = 0 also) into the other five shapes shown on that page. Using Tables 23-A and 23-B as examples, readers could generate the input and output for all six of those curves by using A = B at 100 cSv and by using the values of m' and m" shown in each figure.
A very important point is that shapes in Figure 23-Eye have actually been reported in the literature for certain dose-responses.
The shape shown by Figure 23-Eye-5, for instance, closely resembles the shape of dose-response shown in Ncrp80 Figure 4.12 for specific-locus mutation frequencies versus X-ray dose in mouse spermatogonia. It also resembles, in shape (not in scale), the dose-response shown in Ncrp80 Figure 9.1 for the incidence of myeloid leukemia in male RF mice versus dose, over a wide range of X-ray or gamma-ray doses.
Figure 23-Eye-6 -- with its initial rise followed by a flattening which is then followed by a secondary rise -- has the same pattern as a number of cell-transformation studies, such as those done by Hall and Miller with C3H10T1/2 mouse cells (Ha81). A similar shape was reported by Preston and Brewen in studies of translocations in mouse spermatogonial cells (Pres73).
A Warning about Other Species and about Cell-Studies :
In the previous chapter, we showed that, (through mid-1989) the radiation committees have over-ruled direct human epidemiological evidence on the shape of dose-response for solid cancers, in favor of generalizations from non-human evidence and from cell studies. (Breast-cancer is the significant exception to this practice.)
The errors which may be inadvertently introduced, by extrapolating from one species to another, are well known. What may be less fully appreciated by some readers are the serious confounding variables even within a single species. So we will provide an illustration, described by Little (Li81), in which an experimental dose-response was converted from concave-upward to linear, by changing the chemical milieu of the irradiated cells.
Little described experiments (Terz76; Kenn78) using mouse 10T1/2 cells to study cell transformation (from normal to cancerous). When the mouse cells were irradiated with various doses of X-rays, a clearly concave-upward dose-response was observed.
However, when the irradiated cells were exposed to the promoting agent commonly known as TPA (12-O-tetradecanoyl-phorbol-13-acetate) during the post-irradiation expression-period, two changes were observed. First, an enormous increase in transformation-yield per surviving cell occurred at all radiation doses. And second, the shape of dose-response changed from concave-upward to perfectly linear.
Such cell-transformation data confirm that the biochemical milieu in which cell cultures are grown can profoundly influence the shape of the dose-response which investigators will observe. This is well known now, and probably explains much of the apparent inconsistency of results reported from experimental work, even within a single species.
In short, biochemical milieu makes a huge difference in dose-response, and if the biochemical milieu of human cells in a laboratory is unnatural -- and it is -- there is no guarantee that cells in intact human beings will have the same dose-response which they have in someone's laboratory.
Without denigrating the valuable experimental work done in laboratories, we simply remind readers that the only reliable data on human dose-response for radiation carcinogenesis are necessarily the human epidemiological data themselves.
5. Proper Risk-Estimates for Low Acute Exposures
We have worked our way back, now, to the title of this chapter.
We have demonstrated that there is no conflict between human epidemiology (which shows a supra-linear or linear dose-response, but not a concave-upward one) and the hypothesis from radiobiology that intra-track carcinogenesis can be expressed by a positive linear term, and inter-track carcinogenesis by a positive quadratic term.
The absence of conflict follows from the fact that the linear-quadratic hypothesis does not necessarily predict a concave-upward dose-response. It can predict any of the shapes (and more) which are depicted in Figure 23-Eye. It can certainly predict a supra-linear or linear dose-response, as we have shown -- provided that analysts exclude artificial constraints, such as the presumption that the cell-inactivation term can operate only at very high doses.
Curve-Fitting to the Real Evidence :
There is a great deal of experimental evidence (from other species and cell studies), as well as the direct human evidence itself, which confirms that the LQ model needs an exponential modifier -- as shown in Equation (4) -- in order to fit actual observations.
It is crucial that the values and signs (positive, negative) for m' and m" in the exponential modifier be chosen in order to fit the observations. It is the antithesis of objectivity for anyone to pre-judge these values, and then to discard reality-based observations if they do not fit the resulting curve.
Moreover, Figures 23-D through 23-Eye show that the LQ hypothesis would not be violated if it should turn out that dose-response for radiation carcinogenesis is concave-downward for some species (e.g., the human) and concave-upward or some other shape for other species. Such variation would be perfectly consistent with species-specific variation in values of m' and m".
It is difficult to understand why this point has not been emphasized by the radiation committees for the past ten years. Instead, they have repeatedly suggested that analysts must choose between "radiobiology" and human epidemiological evidence, as if a conflict existed. We have shown that radiobiology and epidemiology can be in complete harmony with each other regarding the LQ hypothesis.
Risk Increase-Factors Needed :
We and the radiation committees (see for instance Un88, p.415, para.62) are in agreement that the best human epidemiological evidence on the shape of dose-response comes from the A-Bomb Study, for the reasons described in our Chapter 4. And within the A-Bomb Study, analysis for all cancers combined is, of course, far more reliable than single-site analysis.
For three consecutive follow-ups (1950-74, 1950-78, 1950-82), the A-Bomb Study has shown that the dose-response for acute exposure is not concave-upward. Within the data, dose-response for all cancers combined is supra-linear throughout the dose-range. (Beyond 1982, the data are not yet available for anyone to do a "constant-cohort, dual-dosimetry" analysis.)
The absence of a concave-upward dose-response means that risk reduction-factors are completely inappropriate for making risk-estimates at low acute exposures. Supra-linearity means that risk increase-factors would be needed, if one insisted on estimating low-dose risks from high-dose data.
Illustrative Risk Increase-Factors :
Like risk reduction-factors, risk increase-factors derive from the ratio of the steeper linear slope over the lower linear slope (see Part 2).
Supra-Linearity, with A = B at 400 cSv :
Suppose Figure 23-D described reality, but one had datapoints only at 160 cSv and at zero dose. A linear interpolation, between 160 cSv on Plot M and the origin, would have the slope of 44,600.9 (from Table 23-C, Column C at 160 cSv) over 160 cSv, or 278.8 cancers per cSv. At low doses, the actual slope of Plot M, however, is almost identical with the unmodified slope of Plot A.
This can be verified by comparing low-dose entries in Column A with the corresponding entries in Column C of Table 23-C. The congruence at very low doses is expected, since the unmodified Column B makes only a small contribution to cancers, and the value of the cell-inactivation term is close to 1.0 at low doses (see Table 23-A).
Thus one can use the slope of the unmodified Plot A to approximate the slope of Plot M at low doses. The slope is 64,000 / 160, or 400. The appropriate risk increase-factor, under these particular circumstances and values of m' and m", would be 400 / 278.8, or 1.43.
Supra-Linearity, with A = B at 50 cSv :
Under these circumstances and with the values of m' and m" used in Table 23-B, the linear slope of Plot M between 160 cSv and the origin would be 4361.97 (from Table 23-B, Column D) over 160, or 27.26. The slope of the unmodified Plot A would be 8000 / 160, or 50. The risk increase-factor would be 50 / 27.26, or 1.83.
No Need to Use "Factors", Up or Down :
Section 4 of this book clearly shows that direct observations exist along the dose-response curve right down to 10-15 cSv (rems) of acute internal organ-dose. There is simply no need for anyone to use "factors" (up, or down) to estimate low-dose cancer-risk from high-dose data.
If "factors" are invoked anyway, we have shown that risk increase-factors are needed for low acute exposures -- not risk reduction-factors.
6. Risk-Estimates for Slow Delivery of High Doses
The observation of a supra-linear dose-response from acute exposure rules out risk reduction-factors for low acute exposures, but supra-linearity does not automatically rule out the possibility that a high dose is less carcinogenic if it is delivered slowly, than if it is delivered all at once. The various possibilities receive some quantitative examination in Part 6, here, for slow delivery of a high dose. Slow delivery of low doses is examined separately, in Part 7.
Lack of Conclusive Evidence for Moderate and High Doses :
I am not convinced that existing human epidemiological data are capable of reliably quantifying a dose-rate effect -- if one exists at all. It will not be an easy question to settle. If different human studies involve exposure to different distributions of gamma or X-ray energies, and if there is no reliable way to evaluate a valid RBE between such radiations, then a uncertainty factor of about 2 could be introduced on this basis alone. Moreover, dosimetry would have to be excellent.
The breast-cancer fluoroscopy studies cited in Chapter 21 are very reliable for testing whether or not all cancer-response was eliminated by flawless repair, but that is a totally different matter from asking those studies to tell us the exact magnitude of cancer-risk per rem -- well enough to discern a possible effect from dose-rate.
As for experimental data on a dose-rate effect, they are far from conclusive. Some results clearly challenge the conventional assumption that dose-fractionation or very slow delivery reduces the carcinogenic risk, compared with the risk from acute delivery of the same dose. For illustrative purposes, we will mention one such report on cell transformation following irradiation, by Hall and Miller (Ha81). They describe the complicated responses which have been observed with fractionation of X-ray dose (emphasis in the original):
"Experiments with fractionated doses of X-rays indicate that dividing the dose into two equal fractions separated by 5 hr results in a decrease of transformation incidence compared with a single exposure of the same total dose for doses above 1.5 Gy, but that at lower dose levels splitting the dose enhances transformation incidence. In a further series of experiments, it has been shown that the transformation incidence resulting from a dose of 1 Gy delivered in two, three, or four equal fractions spread over 5 hr increases progressively with the number of fractions compared with the same total dose delivered in a single exposure. The same is true for continuous low-dose-rate irradiation, where 1 Gy delivered over 6 hr resulted in more transformations than an acute exposure of the same dose. Thus it has been clearly demonstrated with this in vitro system that the temporal distribution of dose, in particular its protraction over a period of time, significantly enhances transformation incidence at relatively low doses" (Ha81, p.208).
In my opinion, the combination of experimental work, human epidemiology, and hypothetical considerations, does not yet tell us whether dose-rate has any effect on human cancer-risk, when the total dose delivered is moderate or high.
As we shall see in Part 7, however, when the total dose is low, no basis exists for postulating a reduced cancer-risk from slow delivery.
Some General Considerations :
The presumption of the LQ model is that the Q term represents inter-track carcinogenesis. When we compare Column B (the Q term) with Column A+B in Tables 23-B and 23-C, we see that -- at low doses -- inter-track carcinogenesis contributes very little to total excess cancer. The linear term (single tracks, acting independently) accounts for virtually all of the radiation-induced cancer from low acute doses.
Therefore, if a high total dose like 100 cSv is delivered as a series of low doses -- say, one cSv per exposure -- it is widely presumed that the cancer-risk per cSv is reduced, because the inter-track contribution is virtually eliminated (see, for instance, Ncrp80, p.15).
As we illustrate how this presumption operates, it will become evident that a great deal depends upon the relative prominence of the linear and the quadratic terms in the LQ equation. We will evaluate slow versus fast delivery of 100 cSv, for the case where A = B at 400 cSv and, separately, where A = B at 50 cSv.
We will illustrate a range of risk reduction-factors, first by using the common -- but mistaken -- presumption that human dose-response is concave-upward, and then by using the real-world observation that it is not.
With a Concave-Upward
Dose-Response and 100 cSv Total Dose :
If A = B at 400 cSv and b = 1.0, then Table 23-C, Column A+B, shows that excess cancers = 50,000 at 100 cSv of acute dose. The inter-track term (Column B) is contributing substantially -- 10,000 out of 50,000. But the same table shows that cancer-risk from one cSv of dose is 401, to which the linear term contributes 400 cancers and the inter-track term contributes only 1.0.
We can neglect the inter-track term and can say that the risk, from 100 doses of one cSv each, would be (100 x 400 cancers), or 40,000 cancers -- instead of 50,000. Therefore, the risk from slow delivery would be (40,000 / 50,000), or 80 % of the risk from the same dose acutely delivered.
If A = B at 50 cSv and b = 1.0, then Table 23-B, Column A+B, shows that excess cancers = 15,000 at 100 cSv of acute dose. The inter-track term (Column B) is contributing very substantially -- 10,000 out of 15,000. But the same table shows that cancer-risk from one cSv of dose is 51, to which the linear term contributes 50 cancers and the inter- track term contributes only 1.0.
Again we can neglect the inter-track term and can say that the risk, from 100 doses of one cSv each, would be (100 x 50 cancers), or 5,000 cancers -- instead of 15,000. Therefore, the risk from slow delivery would be (5,000 / 15,000), or 33.3 % of the risk from the same dose acutely delivered.
With a Concave-Downward
Dose-Response and 100 cSv Total Dose :
If one accepts the linear-quadratic hypothesis, it follows that when dose-response is concave-downward, one is dealing with Equation (4) -- the modified LQ equation with the cell-inactivation term. At low doses, the quadratic term virtually disappears and only the linear term operates -- and so the cell inactivation term operates essentially on the linear term alone.
But we must ask, "Which cell-inactivation term?" It seems clear that the appropriate choice of cell-inactivation term is dependent upon the rate of delivery of the radiation. Therefore, if 100 cSv is delivered acutely, then the cell-inactivation term, for any particular choice of m' and m", will be found on the line for 100 cSv in Table 23-A. However, if 100 cSv is delivered in the form of 100 doses, each of one cSv, then the cell-inactivation term, for those same values of m' and m", will be found on the line for 1 cSv in Table 23-A.
The consequences of these presumptions will be demonstrated with specific examples.
If A = B at 400 cSv :
Excess cancers will be calculated for acute delivery of 100 cSv, and for 100 cSv delivered in 100 separate doses, each of 1 cSv. The entries from Table 23-C, Column C, will be used. The cell inactivation values will be obtained from Table 23-A, Column D. Those values for the active fraction of cells remaining are:
For dose = 1 cSv: Active fraction = 0.99502
For dose = 100 cSv: Active fraction = 0.63128
For acute delivery of 100 cSv:
A + B = 50,000 (from Table 23-C)
Excess cancers = (50,000)(0.63128)
= 31564
This value is in Column C of Table 23-C.
No Reduced Cancer-Risk :
The conclusion is that there is no protection (no reduced cancer-risk) from slow delivery of 100 cSv in this case. We stress "in this case" because this result is obtained for the case where A = B at 400 cSv, and for a particular set of m' and m" values, chosen to illustrate a concave-downward dose-response.
Intuitively, we are not surprised at the result. When the linear term is so much more important than the quadratic term -- that is, where B does not reach a contribution equal to that of A until a dose of 400 cSv -- the lessening of the quadratic response with dose-delivery in small increments is far smaller than it would be in the case where A = B at some much lower value, e.g. 50 cSv. Indeed, we shall now explore that case.
If A = B at 50 cSv :
Excess cancers will be calculated for acute delivery of 100 cSv, and for 100 cSv delivered in 100 separate doses, each of 1 cSv. The entries from Table 23-B, Column D, will be used. The cell inactivation values will be obtained from Table 23-A, Column H. Those values for the active fraction of cells remaining are:
For dose = 1 cSv: Active fraction = 0.98513
For dose = 100 cSv: Active fraction = 0.25666
For acute delivery of 100 cSv:
A + B = 15,000 (from Table 23-B)
Excess cancers = (15,000)(0.25666)
= 3849.9
This value is in Column D of Table 23-B.
Yes, Reduced Cancer-Risk :
By contrast, the expectation from acute delivery of 100 cSv, for this case, is 3849.9 excess cancers (above).
Therefore, under these circumstances and assumptions, we would invoke a risk-reduction factor of (2623.445 / 3849.9), or 0.68, for slow delivery of 100 cSv.
Summary on Slow Delivery of 100 cSv :
We have shown in Part 6 that estimates of risk reduction-factors, for slow delivery of 100 cSv compared with acute delivery, are affected not only by the shape of the acute dose-response, but also by the dose at which the linear and quadratic terms (A,B) are presumed to be equal.
It may not be appropriate to invoke any risk reduction-factors at all, for slow delivery. Above, under the concave-downward dose-response, we provided one illustration where the presumption of risk reduction-factors would not be warranted under the linear-quadratic model, and one illustration where it would be warranted.
Pending more evidence on this issue, we regard it as premature for anyone to count on a much lower cancer-risk from 100 cSv slowly delivered than from 100 cSv acutely delivered. As we said at the outset of Part 6, we do not believe the issue can yet be settled, for moderate and high total doses, on an objective scientific basis.
7. Risk-Estimates for Slow Delivery of Low Doses
We have already shown, in Section 5 of this book, that there is no dose or dose-rate which is safe, with respect to induction of fatal human cancer.
However, Section 5 did not examine the possibility that low doses received slowly might be less carcinogenic than the same low doses received acutely. Now, in Part 7, we shall show why risk reduction-factors are not appropriate for slow delivery of low total doses.
Doses in the Range of Millirems :
It is unnecessary to look at this issue below 100 millirems. Readers who refer back to Chapter 20 (especially Part 3 and Table 20-M) will see that, at the level of the cell-nucleus, a few hundred millirems can be regarded as the slowest conceivable dose-rate.
Since in the very low dose-range, we are dealing with essentially a single track through a nucleus, there is no difference in dose-rate between a few hundred millirems delivered all at once, and the same total dose spread out over years. In both cases, the dose-rate is virtually instantaneous delivery of the entire dose to those cell-nuclei which receive any dose at all.
It follows that in the entire dose-range between zero dose and a few hundred millirems, the issue is already settled about possible risk-reduction from slow delivery: There is no reduction of risk to be considered because there is no reduction in dose-rate.
Next, we shall consider a somewhat higher dose.
Slow Delivery of 5 cSv :
Using the approach demonstrated in Part 6, we will examine the possible risk-reduction if a total dose of 5 cSv is delivered in five fractions of one cSv each.
If A = B at 400 cSv :
Excess cancers will be calculated for acute delivery of 5 cSv, and for 5 cSv delivered in 5 separate doses, each of 1 cSv. The entries from Table 23-C, Column C, will be used. These are entries for a dose-response which is concave-downward between zero and 5 cSv. The cell-inactivation values will be obtained from Table 23-A, Column D. Those values for the active fraction of cells remaining are:
For dose = 1 cSv: Active fraction = 0.99502
For dose = 5 cSv: Active fraction = 0.97541
For acute delivery of 5 cSv:
A + B = 2,025 (from Table 23-C)
Excess cancers = (2,025)(0.97541)
= 1975.20
This value is in Column C of Table 23-C.
Dose- Active Excess Increment Fraction Cancers ------------------------------------------------ First 0.995020 399.0030 Second 0.990064 397.0157 Third 0.985134 395.0387 Fourth 0.980228 393.0714 Fifth 0.975346 391.1137 Total Excess Cancers 1975.243
We could have made the same calculation here as we did for the case of 100 separate 1 cSv doses:
The average active fraction = 0.985158
Excess cancers = 5 x 401 x 0.985158
= 1975.242
For A = B at 400 cSv, the fast delivery and the slow delivery of 5 cSv yield identical results.
We shall now examine this same comparison, of slow versus fast delivery of 5 cSv, for the case where the quadratic component is more prominent.
If A = B at 50 cSv :
Excess cancers will be calculated for acute delivery of 5 cSv, and for 5 cSv delivered in 5 separate doses, each of 1 cSv. The entries from Table 23-B, Column D, will be used. These are entries for a dose-response which is slightly concave-upward between zero and 5 cSv. The cell inactivation values will be obtained from Table 23-A, Column H. Those values for active fraction of cells remaining are:
For dose = 1 cSv: Active fraction = 0.98513
For dose = 5 cSv: Active fraction = 0.92807
For acute delivery of 5 cSv:
A + B = 275 (from Table 23-B)
Excess cancers = (275)(0.92807)
= 255.219
This value is in Column C of Table 23-C.
Dose- Active Excess Increment Fraction Cancers -------------------------------------------------------- First 0.985130 50.24163 Second 0.970481 49.49454 Third 0.956050 48.75855 Fourth 0.941833 48.03351 Fifth 0.927828 47.31926 Total Excess Cancers 243.8475
We could have made the same calculation here as we did for the case of 100 separate 1 cSv doses:
The average active fraction = 0.956264
Excess cancers = 5 x 51 x 0.956264
= 243.847
By contrast, the expectation from acute delivery of 5 cSv, for this case, is 255.219 excess cancers (above).
Therefore, under these circumstances and assumptions, we would expect cancer-risk from slow delivery to be (243.8474 / 255.219), or 95.5 % of the risk from acute delivery of the same dose -- a negligible difference by most standards.
Summary on 5 cSv :
So at one extreme, where A = B at 400 cSv, the LQ model suggests no risk-reduction factor at all, and at the other extreme, where A = B at 50 cSv, the LQ model suggests a risk reduction-factor of approximately 0.95 .
Slow Delivery of 1.0 cSv :
Lastly, we will temporarily ignore our own remarks, "Doses in the Range of Millirems," in order to push this other approach below 1.0 cSv.
We will compare 1 cSv of acute delivery with ten doses of 0.1 cSv each, for the case where A = B at 50 cSv. Since Table 23-A, Column H, and Table 23-B do not include values for 0.1 cSv, we provide them below:
Active fraction = 0.998501
(A+B) = (5 + 0.01) = 5.01 cancers
Dose Active Excess Increment Fraction Cancers ----------------------------------------------- First 0.99850 5.00249 Second 0.99700 4.99499 Third 0.99551 4.98750 Fourth 0.99402 4.98003 Fifth 0.99253 4.97256 Sixth 0.99104 4.96511 Seventh 0.98955 4.95767 Eighth 0.98807 4.95023 Ninth 0.98659 4.94281 Tenth 0.98511 4.93540 Total Excess Cancers 49.68880
So we can check the calculation as follows:
Excess cancers = 10 x 5.01 x 0.991792
= 49.68880
For comparison, the expectation from acute delivery of 1 cSv, for this case, is 50.2414 excess cancers (from Table 23-B, Column D).
Therefore, under these circumstances and assumptions, we would expect cancer-risk from slow delivery of 1 cSv to be (49.6888 / 50.2414), or 98.9 % of the risk from acute delivery of the same total dose.
In other words, this final fractionation hardly alters the expected risk at all. Thus this analysis is in good accord with the conclusion from track-analysis concerning the meaning of dose-rate at very low tissue-doses (Chapter 20, Part 3).
Slow Exposure -- Validity of Our Cancer-Yields :
Earlier in this book, we have stated that our low-dose Cancer-Yields are applicable to both acute-low and slow-low exposure. Those Cancer-Yields are based on the best-fit curve for acute exposure at 5 cSv (rems) of internal organ-dose. The analyses above indicate that this conclusion -- applicability to both acute-low and slow-low exposure -- is well supported by considerations related to the linear-quadratic model of dose-response.
Indeed, the expectation that there is no meaningful difference between acute and "slow" delivery of radiation dose, in the dose-region of zero to 5 cSv, is consistent with the near convergence in Table 23-B of the unmodified linear term alone (Column A) with the modified linear-quadratic term (Column D), and with the same near convergence in Table 23-C of Column A with Column C, in this dose-region.
It is not possible to state, within the evidence available currently, whether the human data are more consistent with A = B at 400 cSv, or with A = B at 50 cSv. In either case, the analyses above, in Part 7, indicate that no meaningful error at all will be introduced by use of our low-dose Cancer-Yields both for acute and for "slow" delivery of radiation dose.
A Warning about Risk Underestimates :
By contrast, meaningful underestimates of aggregate cancer-risk could develop if low doses, slowly received, were simply ignored -- as currently discussed under "de minimis" and "below regulatory concern" notions (see Chapter 24, Parts 9 and 10).
As shown by Sections 5 and 6 of this book, we cannot find any scientific justification within the evidence for excluding such exposure from risk-estimates or from associated protective measures. We have shown that the per-rad risk from acute-low and slow-low exposure is just as great or even greater than the per-rad risk from acute-moderate or acute-high exposure.