Analysis and Results by the Cancer Difference Method
This chapter is arranged in seven parts:
Logic of the Cancer Difference Method, p.1 Calculation of the Minimum Fatal Cancer-Yield, p.2 Discussion of the Minimum Values, p.3 A Warning about X-Ray Exposure versus Gamma-Ray Exposure, p.4 Radiation-Induced Cancer Demonstrated at 11 and 15 Rems (cSv), p.4 Lifetime Fatal Cancer-Yield -- Calculation and Discussion, p.5 The Bottom Line from the Cancer Difference Method, p.7
Then tables.
Then figures.
1. Logic of the Cancer Difference Method
In Table 13-A, readers will find all the input-data which are required for using the Cancer Difference Method to extract the Minimum Fatal Cancer-Yield from the evidence provided by the A-Bomb Study, 1950-1982. The data are comprehensive, and include both cities, both sexes, all ages, and all cancer-sites (leukemia excluded). Readers will notice that there are entries (Columns B and C) for both dosimetries. This is the next step in demonstrating our "constant-cohort, dual-dosimetry" proposal for handling the A-bomb database.
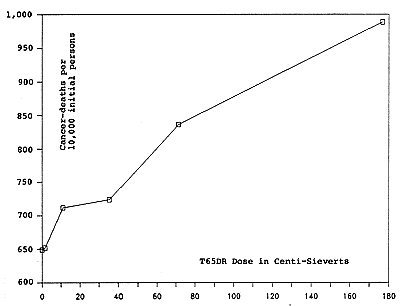
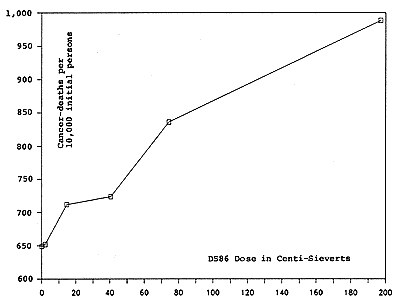
The data from Rows 1 through 6 are the input for Figures 13-A and 13-B, which plot cumulative cancer death-rate per 10,000 initial persons versus dose.
The Cancer Difference Method says: If we compare two groups of people who are alike in their cancer-risk, except for their radiation doses, and if their cumulative cancer death-rates per 10,000 initial persons are truly different, then the difference in cancer-rate is due to the difference in radiation dose.
If the higher cancer-rate is associated with the higher dose, then the difference in cancer-rate (the excess cancer-rate) is the radiation-induced cancer-rate. When we divide the difference in rate per 10,000 initial persons by the difference in dose, we are obtaining the radiation-induced cancer-rate among 10,000 persons of mixed ages, per centi-sievert of average dose (whole-body internal organ-dose). This quantity is, by definition, the Minimum Fatal Cancer-Yield.
It is not necessary for the Reference Group to have no dose at all, since the difference in cumulative cancer death-rate between any two compared groups will be divided by the difference in dose (not by the entire dose of the group with higher exposure).
The Cancer Difference Method can also provide an initial look at the dose-response relationship. An issue of central importance in evaluating the cancer hazard from ionizing radiation is whether the hazard per centi-sievert is lower at low total doses, is the same at all total doses, or is higher at low total doses.
If we pick one class of people as the Reference Group, and then compare it serially with groups which received progressively higher doses, we can discover whether Cancer-Yield stays the same as total dose increases, or whether Cancer-Yield changes in a single direction as total dose increases. Therefore, we are going to compare six exposed groups (Table 13-A, Rows 8-13) with the Reference Group.
Except for Dose-Group 3, which is big enough to stand alone in terms of statistical strength, the exposed groups in Rows 8-13 consist of combinations. Adjacent Dose-Groups have been combined, as indicated by Column A, Rows 9-13, to reduce the relative instability of the observations in E4, E5, and E6. In Row 10, all of the exposed groups have been combined into a single class, and it, too, will be contrasted with the Reference Group.
An Easy Task :
It is hard to imagine an easier task than making these comparisons -- now that the input has been properly prepared. In Chapters 9 and 10, readers have seen the work required to obtain the average organ-doses for all eight of RERF's Dose-Groups, and in both dosimetries. In Chapter 11, readers have seen the work required to overcome the fact that the people in RERF's eight Dose-Groups were not "alike except for radiation doses"; in the raw data, the distribution of ages and sexes differed from Dose-Group to Dose-Group.
Now there is only one more requirement to meet: The cancer death-rates in compared groups must be truly different, and not explicable as random differences in sampling (sampling variation). Statistical testing in Chapter 27 has demonstrated that each of the six exposed groups in Rows 8-13 shows a significantly higher cumulative cancer-rate than does the Reference Class. We wish to stress that such tests are reliable because they were made on the normalized numbers of cancers, not on the raw numbers. So, with the assurance that cancer death-rates are truly different in the groups to be compared, the final requirement for analysis by the Cancer Difference Method has been met.
2. Calculation of the Minimum Fatal Cancer-Yield
We are going to illustrate the calculation of Minimum Fatal Cancer-Yields by making three of the six comparisons, in the T65DR dosimetry. For the T65DR dosimetry, calculations take the data from Columns B and F of Table 13-A, whereas for the DS86 dosimetry, calculations take the data from Columns C and F. In "constant-cohorts," there is only one set of cohorts and thus only one set of cancer-rates (Column F).
o STEP 1: We are asking this question, "How big is the difference in cancer death-rate between the Reference Group and the Low, Mid, and High Dose-Groups?" So, we take the rates from Rows 7, 8, 11, and 12 of Table 13-A:
Column 1 Column 2 Column 3
---------- ---------- ----------
Low-Dose Exposed minus
Reference Class, = 712.02 minus 650.80 = 61.22
in cancers / 10,000
Mid-Dose Exposed minus
Reference Class, = 771.60 minus 650.80 = 120.80
in cancers / 10,000
High-Dose Exposed minus
Reference Class, = 909.57 minus 650.80 = 258.78
in cancers / 10,000
Chapter 11 established that it is appropriate to regard the residual differences in cancer-rates per 10,000 initial persons (Column 3) as having been caused by the radiation dose-difference between classes.
o STEP 2: So the next question is, "How big (how many rems or cSv) are the dose-differences?" We take the doses from Column B, Rows 7, 8, 11, and 12 of Table 13-A:
Low-Dose Exposed minus Reference Class, = 10.994 minus 0.659 = 10.335 in rems (cSv) Mid-Dose Exposed minus Reference Class, = 50.653 minus 0.659 = 49.994 in rems (cSv) High-Dose Exposed minus Reference Class, = 122.056 minus 0.659 = 121.397 in rems (cSv)
o STEP 3: We calculate the radiation-induced cancer-rates per rem (cSv):
Comparing Radiation-induced cancer-rate 61.22 Low-Dose ----------------------------- = ------ = 5.92 with Ref. Difference in dose 10.335 Comparing Radiation-induced cancer-rate 120.80 Mid-Dose ----------------------------- = ------ = 2.42 with Ref. Difference in dose 49.99 Comparing Radiation-induced cancer-rate 258.78 High-Dose ----------------------------- = ------ = 2.13 with Ref. Difference in dose 121.40
The analysis is complete for those three comparisons. For three different dose-levels, we have the Minimum Fatal Cancer-Yield, namely the cumulative number of radiation-induced cancer-fatalities which have already occurred (1950-1982) among 10,000 persons of mixed ages, per cSv of whole-body internal organ-dose. Precisely the same steps are used to make the additional comparisons, of course, and the results are entered in Table 13-B, Row 1, Columns B through G.
These are the so-called central values or best estimates. Confidence-limits are provided in Chapter 27, Part 2.
In Row 2 of Table 13-B, the values of Row 1 are increased by the factor of 1.23 used by RERF for underdiagnosis of cancer-death (see the end of Chapter 11).
Columns H through M of Table 13-B present the findings for exactly the same cohorts of persons, when their mean doses have been re-estimated under the current version of the DS86 dosimetry.
The parallel analyses demonstrate the "constant-cohort, dual-dosimetry" approach to maintaining the scientific status of the A-Bomb Study as an objective prospective study, while also examining the implications of a new dosimetry.
3. Discussion of the Minimum Values
Reliability of Input and Method :
Because the data in this chapter remain undivided by cancer-site, age, sex, city, or short periods, they suffer the least possible amount from random differences in sampling. Indeed, combination of various adjacent Dose-Groups has produced datapoints with greater stability than Dose-Groups examined singly. Moreover, all the datapoints used in this analysis remain free from the hazard of unintended distortion by elaborate statistical manipulation and "tortured mathematics" -- a phrase appropriately used in the BEIR-3 Report by its chairman (Edward P. Radford, in Beir80, p.239).
In addition, the Minimum Fatal Cancer-Yields in Table 13-B are independent from any model or hypothesis for radiation carcinogenesis. The values are based exclusively on the count of actual cancer-cases which have already occurred, and which cannot be undone or disputed as "hypothetical."
Comparison of Normalized and Raw Data at Low Doses :
In Chapter 11, after matching RERF's Dose-Groups for age and sex distribution, we stated that the effect of the normalization would be to reduce the estimates of cancer-hazard from low-dose exposure, by comparison with findings based on the raw data. Now we can show in detail how this happens.
Cancer-Yield is a difference in cancer-rate divided by the corresponding difference in dose. The dose-difference is virtually the same in our raw and normalized data. But let us look at cancer-rates.
For low-dose exposure, the relevant rates are in the Reference Group and Dose-Group 3, of course. In the normalized data from Table 13-A, we find that the difference in cumulative cancer death-rates is (712.02 per 10,000 in Dose-Group 3) minus (650.80 per 10,000 in the Reference Group), or a difference of 61.22 cancer-deaths per 10,000 initial persons. What would the difference have been in the raw data?
We can find out most easily by consulting Table 4-A. The rate in Dose-Group 3 is (1055 cancers / 14943 initial persons) x (10000), or 706.02 cancer-deaths per 10,000 initial persons. In the Reference Group (1+2), there are (2376 + 1779), or 4155 cancer-deaths. There are (37173 + 28855), or 66028 initial persons. The rate is (4155 / 66028) x (10000), or 629.28 cancer-deaths per 10,000 initial persons. Therefore, in the raw data, the difference in cancer death-rates would have been (706.02 - 629.28), or 76.74 cancer-deaths per 10,000 initial persons -- which is a greater difference in rate than 61.22, the value from the normalized data.
When the smaller, normalized difference in cancer-rate is divided by a fixed difference in dose, the result is necessarily a smaller increment in cancer-rate per unit dose from the normalized data, than from the raw data -- in other words, a lower Cancer-Yield or risk-estimate.
Comparison of Findings in the T65DR and DS86 Dosimetries :
If one examines Row 1 of Table 13-B, the biggest difference one can find, between results in T65DR and DS86, occurs at the lowest dose-level (entries B1 and H1). There is nothing puzzling about it, in the "constant-cohort, dual-dosimetry" approach.
The individuals in Dose-Group 3, and their observed cancer death-rate, are the same in the two parallel analyses. Likewise, the individuals in the Reference Group, and their observed cancer death-rate, are the same in the two analyses. It follows that the difference in their cancer death-rates is the same in both dosimetries. Indeed, everything is identical in the two analyses except for average dose.
The new dosimetry increases the dose-estimate of the low-dose exposed group from 10.994 rems up to 14.564 rems -- by about 32 percent, which is the largest of any exposed group on a percentage basis (Table 13-A, Rows 1-6). When a fixed difference in cancer-rate is divided by a larger difference in dose, the inevitable consequence is a smaller difference in cancer-rate per unit dose -- in other words, a lower Cancer-Yield or risk-estimate.
Shape of the Dose-Response Relationship :
Along Row 1 of Table 13-B, Cancer-Yield is steadily falling as the dose examined is steadily rising, and this is true in both dosimetries. In other words, everywhere in the dose-range, the average carcinogenic potency per rem of exposure is falling as dose rises.
An approximately constant Cancer-Yield at all dose-levels would suggest the linear dose-response, of course. The observed deviations from constancy in Row 1 are not random at all, however. They occur in a single direction, and strongly suggest a supra-linear dose-response. Figure 13-C contrasts supra-linear vs. concave-upward responses.
In Chapter 14, we shall examine this very important question of shape in quantitative detail. For readers who are curious about shape when cancer-risk is evaluated per 10,000 person-years instead of per 10,000 initial persons, we provide additional analysis and curves in Chapter 30.
Low-Dose Exposures Slowly Delivered :
In Chapters 2222 and 23, we show that there is no basis in logic or in human evidence for thinking that the Minimum Fatal Cancer-Yields for low-dose exposure in Table 13-B would be lower, if the exposures had been slowly delivered instead of acutely delivered.
4. A Warning about X-Ray versus Gamma Exposure
For medical personnel and patients alike, it is important to note that Cancer-Yields based exclusively on the A-Bomb Study may underestimate -- by about two-fold -- the cancer-hazard per rem from X-ray exposures. In other words, the values in Table 13-B may need doubling.
Although both gamma rays and X-rays are classed as radiations of low-LET (Linear Energy Transfer), readers will see later that medical X-rays transfer a given amount of energy in a much shorter range of tissue than do A-bomb gamma radiations (Table 20-Eye, in our Threshold section). Therefore, the RBE of X-rays is probably higher than the RBE of A-bomb gamma rays. (RBE is defined and discussed in Chapter 8, Part 5.)
In some experimental work, others have tried to quantify the extra potency of orthovoltage X-rays compared with gamma rays of higher energy. For instance, Bond and co-workers state that " . . . the RBE of 250-kVp X rays compared to Co-60 gamma rays for low doses and dose rates, appears to be of the order of 2" (Bon78, p.433). Sinclair makes a statement which amounts to suggesting the potency of orthovoltage X-rays is twice as high as the potency of gamma rays, when he suggests that the RBE values for neutrons, which are tied to the classic X-ray base, should be multiplied by a factor of two to adjust for a gamma-ray base (Sin85). Kerr, referring to Sinclair's 1985 review-paper, concurs about the factor of two (Kerr88, p.243-245).
5. Radiation-Induced Cancer Demonstrated at 11 and 15 Rems
Before we calculated the Minimum Fatal Cancer-Yields in Part 2 of this chapter, we demonstrated that there exists a statistically significant difference between the observations in Dose-Group 3 versus the Reference Group. This fact deserves some emphasis, because it is very commonly and very mistakenly asserted in many circles that there is no evidence of radiation-induced cancer occurring in humans below high doses like 50 cSv (rems) or even 100 cSv. (See Index, "Low-dose human data lacking.")
Contrary to such claims, the evidence is conclusive that low-LET doses far lower than 50 cSv -- indeed, far lower than 10 cSv -- have induced cancer in humans (see Threshold section of this book).
Even if we limit discussion in this chapter to the A-Bomb Study, the evidence in Chapter 27, Part 1, is that cancer death-rates are truly different and higher in Dose-Group 3 compared with the Reference Group (Dose-Groups 1 + 2). This finding is consistent with the work by Preston and co-workers (Pr86), who report finding the difference between Dose-Group 3 and Dose-Group 1 (by itself) to be significant. Since the average organ-dose in Dose-Group 3 is 10.994 cSv in the T65DR dosimetry, and 14.564 cSv in the DS86 system, excess cancer has been observed in the A-bomb survivors at these doses -- way below 50 or 100 cSv.
Our testing in Chapter 27, Part 1, yields p-values which are quite low for both the one-tailed and the two-tailed testing. Moreover, our testing is based on the age- and sex-normalized values for cancer cases. It has already been pointed out, in Part 3 of this chapter, that the net effect of normalization was to reduce the gap in cancer-rate between Dose-Group 3 and the Reference Group. So it cannot be said that the normalization process caused the difference in cancer-rates to be significant; the adjustments reduced the likelihood of finding a significant difference.
6. Lifetime Fatal Cancer-Yield -- Calculation and Discussion
Part 2 of this chapter produced Minimum Fatal Cancer-Yields for low-dose exposure which are very solidly grounded in the available evidence for 1950-1982, in both dosimetries. The data which are required to extend the "constant-cohort, dual-dosimetry" analysis to 1985 are not yet at hand (Chapter 6, page 2).
The next question was already described in Chapter 12: How will the ultimate lifetime Fatal Cancer-Yields compare with the minimum Fatal Cancer-Yields now "in-the-box"?
Every analyst who tries to answer this question is necessarily making a prediction. The basis should be careful examination of trends in whatever evidence has already accumulated. Such work is presented in Chapter 17.
How Long Does the Carcinogenic Effect Persist ?
In Chapter 17, readers will see for themselves that the carcinogenic effect of the bombings appears to be increasing with time since the exposures, when all age-bands are considered as a unit. On the other hand, when the study's five age-bands are examined separately, the risk-ratio (of cancer death-rates in the exposed groups over cancer death-rates in the Reference Group) appears to be approximately constant through time. The approximate constancy of this ratio is remarkable, because it occurs even in age-bands where the spontaneous cancer death-rate has been tripling, six-folding, or ten-folding during the first 32 years of follow-up.
If the risk-ratio is approximately constant during the first 32 years of follow-up, it suggests that the carcinogenic effect from exposure is probably lifelong. This interim finding from the A-Bomb Study is compared with interim findings from other studies, in Chapter 17.
Only future follow-ups can resolve the issue with certainty. Meanwhile, analysts must use the best available evidence. Therefore, our Lifetime Fatal Cancer-Yields incorporate the presumption that the carcinogenic effect will persist for the full lifespan after exposure -- because no other presumption can be justified by the evidence so far. Incidentally, RERF analysts are now using the same presumption (TR-9-87, p.34; TR-5-88, p.50).
Basis for the Factor of 2.223 :
Table 13-B, Note 4, states that all the Lifetime Cancer-Yields in the table are obtained by multiplying the Minimum Cancer-Yields by 2.223. Where does this factor come from?
It comes from Table 28-D, Row 14. It is the ratio of the ultimate number of spontaneous cancer-deaths expected beyond 1950 in the Reference Group when all participants have died, over the cumulative number of spontaneous cancer-deaths already observed in this group between 1950-1982. Chapter 28 shows, step by step, how we estimated the ultimate number, which we derived from the observations internal to the A-Bomb Study itself.
And why do we use this ratio to convert Minimum Fatal Cancer-Yields into Lifetime values? The answer will emerge from the assumption and relationships described below.
The key assumption here is that the current risk-ratio (exposed cancer-rate over Reference cancer-rate) will persist unchanged. By current risk-ratio, we mean the ratio which describes the entire 1950-1982 follow-up. For brevity, we can call this current ratio "C." For instance, in the low-dose comparison, Column F of Table 13-A shows that "C" is (712.02 / 650.80), or 1.094. In this chapter, we are using the assumption that this ratio will still be about 1.094 when the full lifespan follow-up is complete. Now we will state the fundamental relationships.
- Let Ref stand for cancer-rate per 10,000 in the Reference Group.
- Let Exp stand for cancer-rate per 10,000 in the radiation-exposed group. (Exp = Exposed.)
- Let C = the current risk-ratio of (Exp / Ref).
- Therefore: Exp = C times Ref, or CRef.
Thus, in Equation (1) below, we can substitute CRef for Exp. Since Minimum Fatal Cancer-Yield is the difference in cancer-rates over the difference in dose, we can write:
o -- Equation (1) for Minimum Fatal Cancer-Yield:
Minimum Fatal Cancer-Yield
= (Exp - Ref) / Dose-Difference.
= (CRef - Ref) / Dose-Difference.If the ultimate spontaneous cancer-rate per 10,000 initial persons is going to become 2.223-fold higher than the cumulative rate through 1982, and if the ultimate risk-ratio of (Exposed Ca-Rate / Reference Ca-Rate) is going to remain "C," then we can write:
Ultimate Ref = 2.223 Ref.
C = (Ultimate Exp / Ultimate Ref).
C = (Ultimate Exp / 2.223 Ref).
Ultimate Exp = C times 2.223 Ref, or 2.223 CRef.
Then we can make substitutions, in Equation (2).o -- Equation (2) for Lifetime Fatal Cancer-Yield:
Lifetime Fatal Cancer-Yield
= (Ult.Exp - Ult.Ref) / Dose-Difference.
= (2.223 CRef - 2.223 Ref) / Dose-Diff.
= (2.223)(CRef - Ref) / Dose-Diff.Comparison of Equations (1) and (2) shows that the Lifetime value would be exactly 2.223 times higher than the Minimum "in-the-box" value, since the dose-difference does not change. And thus one can use the ratio of (ultimate spontaneous cancer-rate / interim spontaneous cancer-rate), which is 2.223, to convert Minimum Fatal Cancer-Yields into Lifetime Fatal Cancer-Yields.
Possible Underestimation of Lifetime Fatal Cancer-Yields :
From the relationships above, it is obvious that an underestimate of the ultimate spontaneous cancer-rate would result in an underestimate of Lifetime Fatal Cancer-Yield, and an overestimate of ultimate spontaneous cancer-rate would result in an overestimate of Lifetime Fatal Cancer-Yield.
It seems more likely that our method in Chapter 28 underestimates the ultimate spontaneous cancer-rate than overestimates it. The basis for this statement is the fact that our method results in the estimate that only 14.5 percent of the initial persons in the Reference Group will ever die of cancer (Table 28-D, entry G13).
This fraction is substantially lower than the fraction suggested elsewhere. In TR-9-87 (p.34) and TR-5-88 (p.53), RERF has suggested "about 20%" as the appropriate "background lifetime risk for all cancer except leukemia in the LSS sample" (LSS means Life Span Study). Japanese vital statistics show that between 1975 and 1983, cancer was accounting for 19 - 23 % of all deaths (So81; Undemo86).
Only time can reveal whether our estimate of ultimate spontaneous cancer-deaths in the Reference Group has, or has not, introduced a serious underestimate into our Lifetime Fatal Cancer-Yields. Obviously if we had a basis right now for believing that a higher value for ultimate spontaneous rate would be scientifically superior, we would have presented a higher value.
Probable Underestimation of Lifetime Fatal Cancer-Yields :
There is a wholly separate reason for treating the Lifetime Fatal Cancer-Yields in Table 13-B as probable underestimates: They come from a method which ignores what is already known about the greater carcinogenic effect of ionizing radiation upon the young than upon the old. From prior analyses (including Go69, Go81, Beir80, Nih85, etc.), we know that the cancer-risk per centi-sievert of dose is higher, the younger the recipient; this conclusion is confirmed again by the 1950-1982 follow-up of the A-bomb survivors (see Chapter 15).
When we look at the raw data in Table 4-B, we see that almost two-thirds of the 91,231 initial participants are still alive at the end of 1982. Also we see that, out of the 6,050 cancers observed so far, 4,659 or 77 % have come from the two age-bands which were oldest at the time of bombing (ATB).
In the normalized data of Table 28-D, we find the same thing in the Reference Group, which was hardly exposed at all. Out of 4,297.08 spontaneous cancer-deaths observed so far (entry H13), the number which comes from the two oldest age-bands is (1018.02 + 631.71 + 925 + 608), or 3,182.73 cases. This is 74 percent of the total. By contrast, the number of spontaneous cancers coming so far from the two youngest age-bands ATB is still extremely low.
As the older age-bands ATB continue passing from the scene, it is self-evident that both the spontaneous and the radiation-induced cancers coming in the A-bomb survivors, beyond 1982, have to come primarily from the younger age-bands -- in great contrast to the source of the cancers observed between 1950-1982.
Thus it is not realistic to assume that the risk-ratio (exposed / Reference Group), as defined earlier in this section, will stay the same beyond 1982 as it was from 1950-1982. The observations prior to the end of 1982 are based on groups with a much lower radiation-risk per centi-sievert than the radiation-risk in the groups which will produce the cancers beyond 1982. In other words, if the carcinogenic effect from exposure is lifelong, the Lifetime Yields in Table 13-B -- and also in Table 14-C -- are unrealistically low.
In Chapter 15, we will examine the age-bands separately (which means confronting the small-numbers problem), and we will make estimates of the Lifetime Fatal Cancer-Yields which do take age-sensitivity into account.
7. The Bottom Line from the Cancer Difference Method
1. This chapter is our first demonstration of the "constant-cohort, dual-dosimetry" approach to adding another dosimetry (DS86) to the A-Bomb Study. Our approach leaves the study's existing doses, structure and cohorts intact. Our approach also means that the findings in Table 13-B are directly comparable in the existing dosimetry (T65DR) and in the current version of the revised dosimetry (DS86).
2. The Minimum and Lifetime Fatal Cancer-Yields are presented in Table 13-B, for exposure of a mixed-age population. The findings are based on the 1950-1982 follow-up. Although RERF possesses additional observations through 1985, the data required to do a "constant-cohort, dual-dosimetry" analysis are not yet available to us.
3. In order to evaluate hazard to a population of mixed ages, from low doses of ionizing radiation, there is no need to extrapolate any results from high to low doses. The evidence in this chapter and Chapter 27 (Part 1) shows that excess cancer (radiation-induced cancer) is provably real at average organ-doses at least as low as 11 to 15 rems (centi-sieverts). The A-Bomb Study -- and several others (see Chapter 21) -- simply invalidate the common claim that there exists no human evidence of radiation-induced cancer below high doses like 50 rems (centi-sieverts) or even 100 rems.
4. The low-dose Cancer-Yields in Table 13-B (Columns B and H), already apply to low-dose exposure, and were not extrapolated from high-dose data. Moreover, as we shall show in Chapter 23, the low-dose Cancer-Yields apply to low doses which are slowly delivered, as well as to low doses which are acutely delivered.
5. The evidence in Table 13-B is that cancer-risk per rem of exposure is more severe at low doses than at high doses. This very important finding will be explored and validated in quantitative detail in Chapter 14 (and also in Chapter 30, for readers who are interested in person-years).
6. Findings in this chapter are extremely solid for Minimum Fatal Cancer-Yields and for the shape of the dose-response relationship, because the data have not been excessively subdivided, and because all the datapoints remain free from the hazard of unintended distortion by elaborate statistical manipulation. In addition, the Minimum Fatal Cancer-Yields in Table 13-B are independent from any hypotheses. The values are based exclusively on the count of actual cancer-cases which have already occurred, and which cannot be undone or disputed as "hypothetical."
7. The estimated lifetime Fatal Cancer-Yields in Table 13-B are unrealistically low, because the method is not the appropriate one for making predictions beyond 1982 (a very different method is used in Chapter 16 to determine the probable Lifetime Fatal Cancer-Yields). Even so, the estimates for low-dose exposure in Table 13-B, entries H4 and B4, are much higher than the lifetime values of 1.0 and 2.0 which have been routinely used by the radiation community for making statements about low-dose exposure.
|==================================================================================| | Col.A Col.B Col.C Col.D Col.E Col.F | | Organ- Organ- Initial Cancer- Cancer | | Dose- Dose Dose Persons Deaths Death-Rate | | Group (cSv). (cSv). Male+Female (except per 10,000 | | RBE = 2 RBE = 20 in Leukemia) Initial | | Row in T65DR in DS86 Dose-Group 1950-82 Persons | |================================================================================= | | | | 1 Group 1 0.000 0.089 37173 2413.68 649.31 | | 2 Group 2 1.511 1.890 28855 1881.04 651.89 | | 3 Group 3 10.994 14.564 14943 1063.97 712.02 | | 4 Group 4 35.361 40.625 4225 305.77 723.72 | | 5 Group 5 71.308 74.238 3128 261.58 836.27 | | 6 Group 6+7+8 176.662 197.054 2907 287.34 988.45 | | | | SUM T65DR DS86 91231 6213.38 | | | |================================================================================= | | | | REFERENCE-CLASS (Dose-Groups 1 + 2) : | | | | 7 Group (1+2) 0.659 0.875 66028 4297.08 650.80 | | | |================================================================================= | | | | THE SIX EXPOSED DOSE-CLASSES TO BE ANALYZED BY THE CANCER DIFFERENCE METHOD : | | | | | | 8 Low-Dose: Group 3 10.994 14.564 14943 1063.97 712.02 | | | | 9 Groups (3+4) 16.365 20.309 19168 1369.74 714.60 | | | | 10 All: (3+4+5+6+7+8) 41.673 47.388 25203 1918.67 761.29 | | | | 11 Mid-Dose: (4+5) 50.653 54.924 7353 567.36 771.60 | | | | 12 High-Dose:(5+6+7+8) 122.056 133.397 6035 548.93 909.57 | | | | 13 Groups (6+7+8) 176.662 197.054 2907 287.34 988.45 | | | |==================================================================================|
All entries in Rows 1 through 13 come from Table 11-H, and are reproduced here for convenience. (See Table 11-H, Note 2, about the slight disparity between entry E7 above and the sum of entries E1+E2.)
Basis: A-Bomb survivors, 1950-82. (Cities, sexes, ages, and all cancer-sites combined. Leukemia excluded.) Cancer-hazard from X-rays may be underestimated by the A-Bomb Study. See this chapter, Part 4.
Cancer-Yields are radiation-induced cancer-deaths among 10,000 persons of mixed ages, per cSv of whole-body internal organ-dose.
====================================================================================================== | [----- Fatal Cancer-Yield -----] || [------ Fatal Cancer-Yield -----] | | T65DR Dosimetry, Neutron RBE = 2.0 || DS86 Dosimetry, Neutron RBE = 20 | | || | | A B C D E F G || H I J K L M | | Ref. Ref. Ref. Ref. Ref. Ref. || Ref. Ref. Ref. Ref. Ref. Ref. | | Basis for vs. vs. vs. vs. vs. vs. || vs. vs. vs. vs. vs. vs. | | Cancer-Yield 11 16 42 51 122 177 || 15 20 47 55 133 197 | |Row cSv cSv cSv cSv cSv cSv || cSv cSv cSv cSv cSv cSv | |=================================================================================================== | | MINIMUM FATAL || | | CANCER-YIELD || | | 1 "IN THE BOX" 5.92 4.06 2.69 2.42 2.13 1.92 || 4.47 3.28 2.38 2.24 1.95 1.72 | |=================================================================================================== | | MINIMUM FATAL || | | CANCER-YIELD || | | "IN THE BOX" || | | Corrected for || | | 2 Underascert. 7.29 5.00 3.31 2.97 2.62 2.36 || 5.50 4.04 2.92 2.75 2.40 2.12 | |=================================================================================================== | | LIFETIME FATAL || | | 3 CANCER-YIELD 13.17 9.03 5.99 5.37 4.74 4.26 || 9.94 7.30 5.28 4.97 4.34 3.83 | |------------------------------------------------------------||------------------------------------- | | LIFETIME FATAL || | | CANCER-YIELD || | | Corrected for || | | 4 Underascert. 16.20 11.11 7.37 6.61 5.83 5.25 || 12.23 8.98 6.50 6.11 5.34 4.71 | ======================================================================================================
For the atomic-bomb survivors, this plot shows cumulative cancer-deaths (1950-1982) per 10,000 initial persons, versus mean whole-body internal organ-dose in the T65DR dosimetry (neutron RBE = 2).
Data for the six observations (indicated by the boxes) are from Table 13-A, Rows 1 through 6, Columns B and F.

For the atomic-bomb survivors, this plot shows cumulative cancer-deaths (1950-1982) per 10,000 initial persons, versus mean whole-body internal organ-dose in the DS86 dosimetry (neutron RBE = 20).
Data for the six observations (indicated by the boxes) are from Table 13-A, Rows 1 through 6, Columns C and F.
This plot shows cancer-response versus dose for exactly the same cohorts of survivors as Figure 13-A. This is the "constant-cohort, dual-dosimetry" approach to the DS86 dosimetry. The only difference between Figures 13-A and 13-B is the mean internal organ-dose assigned to the cohorts. (The dose-scale in this figure extends up to 200 cSv.)
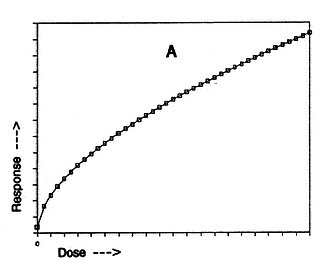
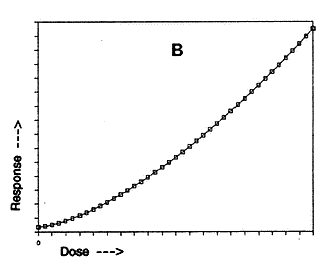
Both curves A and B, below, depict the behavior of a response (for instance, cancer death-rate) as a dose of something increases. The response need not be cancer death-rate, and the "something" need not be ionizing radiation. Curves A and B are just generic dose-response curves.
Curve A = Supra-Linear Curvature :
The shape of Curve A is often called "concave-downward" or supra-linear. It is supra-linear because, if a straight line is drawn between any two points along the curve, the curve will lie above the line.
In a supra-linear dose-response, the risk per unit of dose is highest in the low dose-range. The magnitude of response, per unit of increase in dose, declines with rising dose.
Curve B = Concave-Upward Curvature :
The shape of Curve B is often called "concave-upward." In Curve B, if a straight line is drawn between any two points along the curve, the curve will lie below the line. In a concave-upward dose-response, the risk per unit of dose is lowest in the low dose-range. The magnitude of response, per unit of increase in dose, rises with rising dose.
The dose-response relationship depicted by Curve B is often called "linear-quadratic" -- which is an ambiguous term unless the sign of the quadratic term is specified. When the quadratic term is positive, the shape is concave-upward, but when the quadratic term is negative, the shape is concave-downward. (This is explained in Chapter 23, Part 2.)