Next |
ToC |
Prev
CHAPTER 3
Early-Onset Breast-Cancer: Evidence on Radiation-Induction
An enormously important issue is breast-cancer which becomes
clinically manifest in very young women --- before age 35, for
instance. Recent evidence, discussed below, underscores the
importance of acting upon the finding of this book, if
prevention is everyone's goal. So that all readers (including
the "easy readers") can contemplate the meaning of this new
evidence, we introduce the units in which radiation doses are
measured.
Part 1. Dose-Units, Especially "Medical Rads"
The term "medical rad" is the one which we use in reaching the
finding of this book. To show what it means, we have to cover
some other units.
Rads. The "rad" is a unit in which amounts (doses) of ionizing
radiation are measured, the way "dozen" measures an amount of
eggs. Rad is the abbreviation for "radiation absorbed dose." A
rad is really just a ratio of energy delivered by ionizing
radiation, per gram of irradiated cells or tissue. A rad is 100
ergs of energy per gram --- a definition which no reader needs
to remember. One thousandth of a rad, or 0.001 rad, is a
milli-rad. An effort is underway to re-name the rad as a
centi-gray (cGy) and to call 100 rads a gray (Gy). We and many
others prefer to stick with rads.
Roentgens. The Roentgen is a unit for measuring ionization in
air; a few reports also use it for doses inside the body. The
abbreviation for Roentgen is R (but a small "r" was customary in
the older literature). Under common medical circumstances, an
entrance dose of 1 Roentgen at the skin gives a breast-tissue
dose of about 0.69 rad, when the beam is traveling from
front-to-back of a patient. The Roentgen is the dose-unit often
used to describe x-ray dosage from fluoroscopy. In the
1930-1935 era, many fluoroscopy machines could generate beams
with dose-rates like 100 Roentgens per minute
(Braestrup 1969).
Rems. Another unit is called the rem, an abbreviation for
"roentgen equivalent, man." The rem can indicate that
adjustments have been made for the non-standard "quality" of
some radiations. Usually (but not always) the standard is an
x-ray of 100 to 400 KeV. An effort is underway to re-name the
rem as a centi-sievert (cSv) and to call 100 rems a sievert
(Sv).
Medical Rads. Per rad, gamma rays from an atomic bomb are about
half as harmful as x-rays from medical irradiation, so 1.0 rad
of A-bomb gamma radiation could be called 0.5 rem. We avoid
rems in this book by converting all doses into "medical rads."
Hence, 1.0 rad of A-bomb gamma radiation is called 0.5 medical
rad.
Some Very Common Radiation Dose-Levels
 -
Natural Background Radiation. The typical annual dose from
natural background radiation, excluding doses from inhaled
radon, is about 0.1 rem or 100 milli-rems
(BEIR 1972, p.50;
BEIR 1990, p.18). The
dose per year rises with altitude. Because
the natural background dose is mostly from gamma and cosmic
radiation, its medical equivalent per year is about 0.05 medical
rad (50 medical milli-rads). In a 70-year lifespan, the
cumulative dose is about 3.5 whole-body medical rads. A
whole-body dose is received by all parts of the body, in
contrast to a partial-body dose.
-
Natural Background Radiation. The typical annual dose from
natural background radiation, excluding doses from inhaled
radon, is about 0.1 rem or 100 milli-rems
(BEIR 1972, p.50;
BEIR 1990, p.18). The
dose per year rises with altitude. Because
the natural background dose is mostly from gamma and cosmic
radiation, its medical equivalent per year is about 0.05 medical
rad (50 medical milli-rads). In a 70-year lifespan, the
cumulative dose is about 3.5 whole-body medical rads. A
whole-body dose is received by all parts of the body, in
contrast to a partial-body dose.
The natural dose-rate per minute is of interest, for comparison
with dose-rates from fluoroscopy. Nature's dose-rate per minute
is (0.05 medical rad / year) times (1 year / 525,600 minutes),
or 0.000000095 medical rad per minute from natural background
radiation. If we round this off, it is about one ten-millionth
of one medical rad per minute. At this dose-rate, only a tiny
fraction of cells is irradiated per minute.
 -
Airline Travel. The extra radiation dose, from flying
between the east and west coasts of the USA, is about 0.3
milli-rem (0.0003 rem) per hour of commercial flying. For a
ten-hour roundtrip, the extra dose would be about 3 milli-rems
(0.003 rem). It would require about 3,300 flying-hours to
receive 1.0 extra rem of whole-body irradiation --- equivalent
to about 0.5 extra medical rad. Dose-rates from flying vary
with altitude and latitude.
-
Airline Travel. The extra radiation dose, from flying
between the east and west coasts of the USA, is about 0.3
milli-rem (0.0003 rem) per hour of commercial flying. For a
ten-hour roundtrip, the extra dose would be about 3 milli-rems
(0.003 rem). It would require about 3,300 flying-hours to
receive 1.0 extra rem of whole-body irradiation --- equivalent
to about 0.5 extra medical rad. Dose-rates from flying vary
with altitude and latitude.
Part 2. The Dose Which Doubles the Rate of Early-Onset
Breast-Cancer
Ordinarily in epidemiological studies of cancer-development from
radiation, one faces the "small numbers problem": An
insufficient series of cases in the relatively early follow-up
period to permit a reliable conclusion. So time is allowed to
run, to accumulate additional cases ("statistical power"). And
then all the cases --- short latency and long-latency cases,
combined --- are examined together for such issues as
cancer-increase per rad of dose. But what is lost, within the
accumulated total, is any evaluation of whether the
"early-onset" cases are different from the other cases. From
here on, the cases diagnosed before age 35 will be called
"early-onset" cases.
With follow-up of the A-bomb survivors now complete for 1950
through 1985, there may be enough total cases of breast-cancer
to separate the early-onset cases from the others, and to
compare them for induction-rate per rad of irradiation. In
1993, Charles Land, Masayoshi Tokunaga, and additional RERF
analysts, made a brief report in the Lancet, entitled
"Early-Onset Breast Cancer in A-Bomb Survivors"
(Land 1993). By
extracting the pertinent data from the figure in their 1993
paper, we can tabulate their findings in the
nearby box. They are remarkable results, to say the least!
In their 1993 paper, Land et al are reporting exclusively on
female A-bomb survivors who received the bomb-exposure before
the age of 20 years. Although Land et al do not say so, the
number of females who were exposed by the bombs below age 20 was
approximately 12,000, and their average age at the time of
bombing was about 10 years old (calculated from
Gofman 1990,
Table 26-F). There
are 205 incident cases of breast-cancer,
reported between 1950-1985 for this group. The cases are
segregated by Land et al into two main groups: Women whose
breast-cancers occurred before age 35 years constitute one
group, and women whose breast-cancers appeared after age 35
years, the other group. We repeat: All the women were less
than age 20 at the time of exposure.
In the boxed tabulation, the entries for "fractional increase
... per rad" indicate a spectacular difference between
early-onset cases versus cases occurring at age 35 and beyond.
The difference is treated as real (not spurious) in both Land
1993 and Tokunaga 1994. We
shall propose an explanation of the difference in
Part 4. But here, we will focus on the
breast-dose which, if delivered sometime before age 20, can
double the rate of early-onset breast-cancer. This value can
not change with any future observation of the A-bomb survivors,
because the story for early-onset cases was over when the
youngest survivors (newborn in 1945) passed the age of 35 --- in
1980.
 - Tabulation Based Upon Land et al, 1993.
Average Age Number of Fractional Increase
When Breast- Breast- in Breast-Cancer Rate
Cancer Occurs Cancer over Spontaneous Rate
Cases per rad
-----------------------------------------------------------------
Breast Cancers
Occur Before
Age 35 years 32 years 27 0.136 13.6 %
-----------------------------------------------------------------
Breast Cancers 41 years 80 0.013 1.3 %
Occur After 49 years 85 0.024 2.4 %
Age 35 years 57 years 13 0.017 1.7 %
-----------------------------------------------------------------
Sum of cases, bomb-exposed women 205 cases.
- Tabulation Based Upon Land et al, 1993.
Average Age Number of Fractional Increase
When Breast- Breast- in Breast-Cancer Rate
Cancer Occurs Cancer over Spontaneous Rate
Cases per rad
-----------------------------------------------------------------
Breast Cancers
Occur Before
Age 35 years 32 years 27 0.136 13.6 %
-----------------------------------------------------------------
Breast Cancers 41 years 80 0.013 1.3 %
Occur After 49 years 85 0.024 2.4 %
Age 35 years 57 years 13 0.017 1.7 %
-----------------------------------------------------------------
Sum of cases, bomb-exposed women 205 cases.
The "Doubling Dose" for Early-Onset Breast-Cancer
The dose which doubles the spontaneous frequency of early-onset
breast-cancer is the dose which causes a 100 % increase in its
spontaneous rate. Therefore, to estimate how many rads would
cause a 100 % increase, we divide 100 % by 13.6 % per rad (from
the boxed tabulation). Thus, 7.35 rads, received before age 20,
is the approximate doubling dose for early-onset breast-cancer.
The doubling dose for early-onset breast-cancer is even lower
when we consider medical x-ray radiation, or beta particles of
energy comparable to such x-rays. The medical rad has
approximately two times the effectiveness of A-bomb radiation
from which Land, Tokunaga, and colleagues developed their
findings. Therefore, we must warn that the dose of medical rads
required to double the spontaneous rate of early-onset
breast-cancer must be in the neighborhood of only 3.68 medical
rads, received sometime before age 20. As readers will see in
Sections 2
and 3
of this book, such doses and far higher ones
have been commonly received during childhood from certain
medical procedures --- and we do not mean doses from
radiation therapy after a cancer has already occurred.
Part 3. A Test for Agreement about the Magnitude of Risk
Below, we will show the good agreement between RERF's
quantification of risk (by Land, Tokunaga, et al) and our own
independent analysis of 1990. The "easy readers" of this book
may wish to skip to Part 4 or
Part 5, but others will find Part
3 very interesting.
Our analysis used the data on cancer deaths (all types) from
1950-1982 in the A-Bomb Survivors, and the RERF analysis used
exclusively the breast-cancer incidence from 1950-1985 among the
A-Bomb Survivors. Both analyses (Gofman and RERF) are finding
out the "fractional increase or percent increase above the
spontaneous rate, per rad" --- a concept which we named "the
K-value" simply for the sake of brevity. Tokunaga et al call
the same thing "Excess Relative Risk," or ERR.
Based on the linear dose-response in
15-G and
15-H of
Gofman 1990,
our K-value estimate for females exposed at ages
0-9 years is 0.01922 (the same as 1.922 %). Age 0 means from
birth to the first birthday. For exposure at ages 10-19, the
K-value is 0.01097 (or 1.1 %). When the two values are weighted
by the number of cases, the average is 0.01265, or 1.265 % per
rad for exposure at ages 0-19. This value is for all types of
cancer, combined. For breast-cancer alone, the K-value is 2.524
times the value for combined types
(Thompson et al 1994, pages
S26, S49, S61). Multiplying the 1.265 % per rad for all
cancers, by 2.524 to adjust for breast-cancer alone, we obtain a
K-value of 3.2 % per rad for breast-cancer, when bomb-exposure
occurred at ages 0-19 years.
The comparable K-value from RERF's own analysis is 2.41 % per
rad --- from Tokunaga
1994, p.215, Table VI. RERF's value is
derived from observations of cancer incidence, whereas our value
is derived from observations of cancer mortality. When our 3.2
% is divided by their 2.41 %, we see that one estimate differs
from the other by only 33 % . The two separate analyses are in
remarkably close agreement.
The similarity in estimates is supportive of the concept that,
when extra radiation induces extra cancers, it induces cancers
which are fatal and non-fatal in the same proportion as occurs
without the extra exposure to radiation.
Part 4. Early-Onset Cases vs. Later Cases: Why Such a
Difference?
If readers look back in Part 2 at
the boxed tabulation, they
will see the column for "average age when breast-cancer occurs"
for 205 of the A-bomb survivors irradiated between birth and age
20. For cases diagnosed at an average age of 32, the percent
increase per rad above the spontaneous rate is 13.6 %, whereas
the percent increase per rad is dramatically lower if diagnosis
occurs at the average ages of 41 years, or 49 years, or 57
years.
What accounts for the striking difference? Is there some big
biological difference between the radiation-induction of
breast-cancer for cases which appear before age 35, compared
with the radiation-induction of cases which appear after age
35? Is there some altered response (to irradiation during
childhood) in the irradiated hosts after they pass age 35?
Various possibilities are discussed in
Tokunaga 1994 (pp.221-222).
We propose a relatively simple explanation. Our figure, "Three
Curves with a Story," demonstrates how the observed difference
could arise.
Three Curves with a Story
Curve B = breast-cancer rate in women irradiated below age 20,
by an unspecified dose.
Curve A = spontaneous breast-cancer rate in comparable
non-irradiated women.
Curve C = relative risk (Curve B / Curve A).
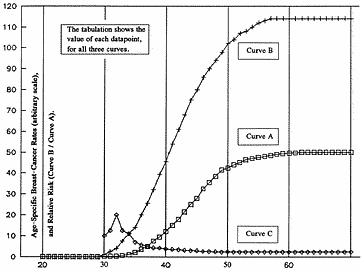
Age at Breast-Cancer Diagnosis, in Years.
Age A B C | Age A B C
---------------------------------+-------------------------------
29 0 0 | 50 42.5 102 2.4
30 0.1 1 10.0 | 51 44.0 104 2.4
31 0.2 2.5 12.5 | 52 45.0 107 2.4
32 0.2 4.0 20.0 | 53 46.5 108 2.4
33 0.6 7.5 12.5 | 54 47.0 110 2.4
34 1.0 11.0 11.0 | 55 47.5 112 2.4
35 2.0 14.0 7.0 | 56 48.0 113 2.4
36 3.5 20.0 5.7 | 57 48.5 114 2.4
37 5.05 25.5 5.0 | 58 49.0 114 2.3
38 7.5 32.0 4.3 | 59 49.3 114 2.3
39 9.5 39.5 4.2 | 60 49.6 114 2.3
40 12.0 45.5 3.8 | 61 49.7 114 2.3
41 15.0 54.0 3.6 | 62 50.0 114 2.3
42 18.0 61.0 3.4 | 63 50.0 114 2.3
43 21.5 68.0 3.2 | 64 50.0 114 2.3
44 25.0 75.0 3.0 | 65 50.0 114 2.3
45 28.0 80.0 2.9 | 66 50.0 114 2.3
46 32.5 86.0 2.6 | 67 50.0 114 2.3
47 35.5 90.0 2.5 | 68 50.0 114 2.3
48 38.5 94.0 2.4 | 69 50.0 114 2.3
49 41.5 98.0 2.4 | 70 50.0 114 2.3
Who Are These Curves?
 -
Curve A: In the nearby
figure, Curve A depicts a
spontaneous breast-cancer rate beginning to rise when women
reach the age of about 30. We wish to emphasize that Curve A is
a "generic" or illustrative curve, with imaginary rates of new
cases (per 10,000 women) on the vertical axis. The
reality-based aspect of Curve A is its depiction of a rise which
is gradual, then steep, and then gradual again.
-
Curve A: In the nearby
figure, Curve A depicts a
spontaneous breast-cancer rate beginning to rise when women
reach the age of about 30. We wish to emphasize that Curve A is
a "generic" or illustrative curve, with imaginary rates of new
cases (per 10,000 women) on the vertical axis. The
reality-based aspect of Curve A is its depiction of a rise which
is gradual, then steep, and then gradual again.
For ages 20 through 29, the spontaneous frequency of
breast-cancer is very low (shown as "zero" rate). Then, for
ages 30, 31, and 32, we have elevated each data-point (really,
data-symbol) slightly above the baseline. At age 33, we show
the rate of new cases starting to increase in each successive
year, with the amount of annual increase greater (steeper)
between ages 35 and 50 than between ages 50 and 60, for
example. The rates plotted as Curve A are tabulated in the box underneath the figure.
 -
Curve B: Curve B depicts the corresponding breast-cancer
rate in a comparable group of women who received
breast-irradiation between birth and age 20. Again, we show
imaginary rates of new cases (per 10,000 women) on the vertical
axis, and we have not specified any particular radiation dose.
What we are showing, however, is reality-based: Starting at age
30, the irradiated group shows a rate of breast-cancer which is
higher than the spontaneous rate. The real-world observations
of a higher rate were discussed in Part 2. Among the irradiated
A-bomb survivors who were ages 0-19 during the bombings, there
are 27 cases of early-onset breast-cancer --- and all but 2 or 3
of those cases were diagnosed when the women were ages 30
through 34 (Tokunaga 1994,
p.214). There are 178 additional cases diagnosed after age 35
in that group.
-
Curve B: Curve B depicts the corresponding breast-cancer
rate in a comparable group of women who received
breast-irradiation between birth and age 20. Again, we show
imaginary rates of new cases (per 10,000 women) on the vertical
axis, and we have not specified any particular radiation dose.
What we are showing, however, is reality-based: Starting at age
30, the irradiated group shows a rate of breast-cancer which is
higher than the spontaneous rate. The real-world observations
of a higher rate were discussed in Part 2. Among the irradiated
A-bomb survivors who were ages 0-19 during the bombings, there
are 27 cases of early-onset breast-cancer --- and all but 2 or 3
of those cases were diagnosed when the women were ages 30
through 34 (Tokunaga 1994,
p.214). There are 178 additional cases diagnosed after age 35
in that group.
What we want to explain is why the percent increase per rad is
so much higher for the cases diagnosed at the average age of 32
(the early-onset cases) than for cases diagnosed later. Curve C
depicts the question.
 -
Curve C: Curve C shows the result when each cancer-rate of
Curve B, for irradiated women, is divided by the corresponding
(and lower) cancer-rate of Curve A, for non-irradiated women.
The values are also tabulated beneath the
figure. These ratios
are the relative rates, or Relative Risks (RR), which quantify
how many times higher the exposed rate is than the spontaneous
rate. We plot the RR values as Curve C, which uses the scale of
the vertical axis as an "all-purpose" scale (just don't say "per
10,000 women").
-
Curve C: Curve C shows the result when each cancer-rate of
Curve B, for irradiated women, is divided by the corresponding
(and lower) cancer-rate of Curve A, for non-irradiated women.
The values are also tabulated beneath the
figure. These ratios
are the relative rates, or Relative Risks (RR), which quantify
how many times higher the exposed rate is than the spontaneous
rate. We plot the RR values as Curve C, which uses the scale of
the vertical axis as an "all-purpose" scale (just don't say "per
10,000 women").
At age 32, the tabulation shows that the irradiated rate is 20
times higher than the spontaneous rate. To transform this
Relative Risk of 20 into percent increase per rad (K-value), we
just subtract 1.0 from the Relative Risk and then divide 19 by
the dose in rads. Example: If the average dose which produced
Curve B were 110 rads, then the fractional increase per rad for
cases diagnosed at age 32 would be (19 / 110 rads), or 0.173 per
rad --- which is the same as 17.3 % per rad.
What Is the "Story" of A, B, and C?
Curves A and B are nice, smooth curves suggesting nothing
biologically exotic. Nonetheless, their relationship generates
a stunning peak in Relative Risk, and therefore in percent
increase per rad, for early-onset cases diagnosed at an average
age of 32. After its peak value of 20, Relative Risk declines
dramatically --- down to 4.3 for diagnosis at age 38, down to
3.0 for diagnosis at age 44, and then remaining above 2.0 for
diagnosis beyond age 44.
What is the meaning of this peak for early-onset cases?
When two curves (for irradiated and non-irradiated groups) have
been near the zero-rate during a follow-up study, the addition
of just a few cancer-cases to one curve earlier than to the
other curve has to cause very high Relative Risks --- even when
the higher rates are not very high at all. Such events are
illustrated for ages 30, 31, and 32 at diagnosis. At age 29 and
younger, the breast-cancer rates are shown as equal in the
irradiated and non-irradiated groups. Curves A and B are right
on top of each other, at the zero-rate. At age 30, both rates
increase a little (see the tabulated
values): Non-irradiated
moves to 0.1 case per 10,000 women, and irradiated moves to 1
case per 10,000 women --- a very low rate compared with what is
coming later. Nonetheless, this slight change means that the
risk goes "overnight" from being equal in both groups, to being
10-fold higher in the irradiated group --- all because of 1 case
per 10,000 women. At ages 31 and 32, additional small changes
drive the Relative Risk to its peak at 20.
In computing Relative Risks, the spontaneous rates are the
denominators of the fractions. As long as the the spontaneous
rates remain near zero, even modest growth in the exposed rates
will generate enormous Relative Risks. The phenomenon does not
happen when analysts look at the women exposed at older ages,
because the spontaneous rate is already well above zero when
analysts begin comparing the irradiated and non-irradiated
groups.
The Key: A Baseline Rate Near Zero
For A-bomb survivors irradiated below age 20 and diagnosed with
early-onset breast-cancer before age 35, the exceedingly high
Relative Risks (and percents increase per rad) are real --- but
their initial magnitudes turn out to be temporary. Relative
risks compute at a less spectacular level as soon as the
spontaneous cancer-rates have their own rapid climb (away from
zero) in the denominator of such ratios. We have been able to
mirror these observations, in a generic way, with Curves A and
B, which generate Curve C. The three curves also mirror the
observation that the less spectacular Relative Risk (for cases
diagnosed after age 40) persists at an approximately constant
level through the 1985 follow-up (see Land's
data in Part 2; confirmation in
Tokunaga 1994, p.221).
In our opinion, "Three Curves with a Story" means this:
Analysts of the A-Bomb Study need not invoke special concepts
about the cancers or the hosts, in order to explain the much
higher Relative Risk observed for early-onset cancer-cases than
for the cases diagnosed at older ages. The observed difference
in Relative Risk, due to radiation, can be explained by the fact
that both curves rise from a baseline rate which is very close
to zero.
True Meaning of "Less Spectacular"
The "less spectacular" Relative Risk really reflects a much
greater number of radiation-induced breast-cancers than the peak
Relative Risk. In figures like ours, it is the area under a
curve which reflects the aggregate number of cases observed.
The area under Curve B minus the area under Curve A reflects the
excess number of cases induced by radiation. Clearly, the
difference in the two areas for ages 30 through 35 is very small
compared with the difference in the two areas beyond age 35. The
"less spectacular" Relative Risk not only endures much longer,
but it reflects the multiplication (by radiation exposure) of a
much higher spontaneous cancer-rate.
Part 5. The Need for Action
How many women who have developed early-onset breast-cancer over
the past half-century know whether or not they were irradiated
in infancy?
We wonder. Readers of this book are going to learn about a very
large number of female children who suffered the fate of such
undesirable irradiation of the breasts --- even before they left
the nursery of hospitals where they were born. Others suffered
nearly the same fate in their first few years of life.
No one can alter the past. But from the past, we can learn the
key to preventing many, many cases of early-onset and later
breast-cancer. Prevention.
Time Would Tell ... And Time Has Told
Once upon a time (1977), the United Nations Scientific Committee
on the Effects of Atomic Radiation, known as UNSCEAR, speculated
that breast-irradiation during infancy and childhood might have
"minimal" cancer-consequences because "only a few breast cells"
exist to be irradiated before puberty
(UNSCEAR 1977, p.389). Since
these few cells must be the progenitors of all future
breast-tissue cells, we rejected that line of reasoning
(Gofman 1981, p.249-250).
In 1994, the issue seems settled. Tokunaga et al
(1994, p.215,
Table VI) report statistically significant excess breast-cancer
rates in the bomb-irradiated women who were ages 0-9 years old
in 1945 --- as well as in the group which was 10-19 years old in
1945. Both groups, each analyzed separately for the period
1950-1985, show the excess. And both groups have much higher
risks per rad than risks for women who were 20 years of age and
older at the time of the bombings.
The Irradiation of Children Today
The era of irradiating children is far from past. The
diagnostic use of x-rays can be extremely helpful in pediatric
medicine. For example, we are aware that a high number of
x-rays may be taken of premature infants and others in neonatal
intensive care units (NCRP
1989). The use of x-rays is also
high in association with birth defects (especially heart
problems). The use of x-rays for children involved in
automobile and other accidents can also be high, especially if
there are insurance battles and lawsuits.
The task mandated by the evidence in this chapter is not to stop
such examinations, but rather, it is to make sure that the
frequency and doses are kept to the minimum really needed. In
Section 4 of this book,
we have some suggestions about what concerned parents,
physicians, and medical schools can do.
# # # # #
Next |
ToC |
Prev
back to PBC |
CNR |
radiation |
rat haus |
Index |
Search
